
【题目】如图1,在平面直角坐标系中,⊙O1与x轴相切于点A(﹣3,0),与y轴相交于B、C两点,且BC=8,连接AB.
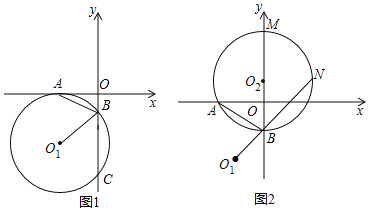
(1)求证:∠ABO1=∠ABO;
(2)求AB的长;
(3)如图2,⊙O2经过A、B两点,与y轴的正半轴交于点M,与O1B的延长线交于点N,求出BM﹣BN的值.
【答案】(1)见解析;(2)AB=![]() ;(3)BM﹣BN的值为2.
;(3)BM﹣BN的值为2.
【解析】
(1)连接AO1根据切线的性质,∠OAO1=90°,因为∠AOB=90°,根据平行线的判定方法,可以判定AO1∥OB,得到∠ABO=∠O1AB,再根据O1A=O1B,即可推导判断出∠ABO1=∠ABO;
(2)过点O1作O1H⊥BC于H,判断出四边形AO1HO是矩形,根据勾股定理求出O1B与AB即可.
(3)作点B关于x轴的对称点B',根据对称性可知OB'=OB=1,AB=AB',根据等角的补角相等得出∠ABN=∠AB'M,根据圆周角定理判断出∠AMB'=∠N,最后判断△AMB'≌△ANB,得出结论MB'=NB,最后计算求解即可.
(1)证明:如图,连接AO1,
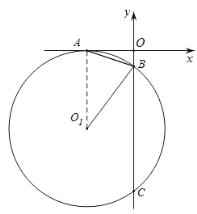
∵⊙O1与x轴相切于点A,
∴∠OAO1=90°,
又∠AOB=90°,
∴∠OAO1+∠AOB=180°,
∴AO1∥OB,
∴∠ABO=∠O1AB,
∵O1A=O1B,
∴∠O1AB=∠ABO1,
∴∠ABO1=∠ABO;
(2)解:如图,过点O1作O1H⊥BC于H,
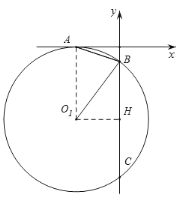
则CH=BH=![]() BC=4,
BC=4,
∴∠O1HO=∠HOA=∠OAO1=90°,
∴四边形AO1HO是矩形,
∴AO1=AO=3,
∴在Rt△O1HB中,
![]() ,
,
∴HO=O1A=O1B=5,
∴OB=HO﹣BH=1,
∴在Rt△AOB中,
![]() ;
;
(3)解:如图,作点B关于x轴的对称点B',则点OB'=OB=1,AB=AB',

∴BB'=2,∠AB'O=∠ABO
∴由(1)知,∠ABO=∠ABO1,
∴∠ABO1=∠AB'O,
∴180°﹣∠ABO1=180°﹣∠AB'O,
即∠ABN=∠AB'M,
又∵![]() ,
,
∴∠AMB'=∠N,
∴△AMB'≌△ANB(AAS),
∴MB'=NB,
∴BM﹣BN=BM﹣B'M=BB'=2,
∴BM﹣BN的值为2.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx-3 (m≠0)与y轴交于点A,其对称轴与x轴交于点B,顶点为C点.
(1)求点A和点B的坐标;
(2)若∠ACB=45°,求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
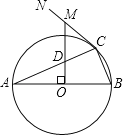
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏东70o方向上,轮船从A处以每小时30海里的速度沿南偏东50o方向匀速航行,1小时后到达码头B处,此时观测灯塔C位于北偏东25o方向上,求灯塔C与码头B之间的距离(结果保留根号).
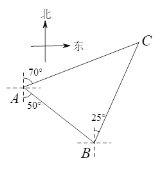
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中有标号为1,2,3,4的四个小球,除数字不同外,小球没有任何区别,摸球前先搅拌均匀,每次摸一个球
(1)摸出一个球,摸到标号为偶数的概率为 .
(2)从袋中不放回地摸两次,用列表或树状图求出两球标号数字为一奇一偶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面![]() 的坡度为
的坡度为![]() ,文化墙
,文化墙![]() 在天桥底部正前方8米处(
在天桥底部正前方8米处(![]() 的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为
的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为![]() .(参考数据:
.(参考数据:![]() ,
,![]() )
)
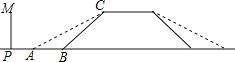
(1)若新坡面坡角为![]() ,求坡角
,求坡角![]() 度数;
度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙![]() 是否需要拆除?请说明理由.
是否需要拆除?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com