
分析 (1)由3x-y=6可得出y=3x-6,代入x=3求出y值即可得出结论;
(2)由$\frac{12}{x-3}$为自然数结合12的因数的个数,即可找出正整数x的个数;
(3)设笔记本买了x本,钢笔买了y支,根据总价=单价×数量,即可得出3x+5y=48,结合x、y均为正整数即可得出二元一次方程的解,再根据方程的解找出各购买方案即可.
解答 解:(1)∵3x-y=6,
∴y=3x-6.
当x=3时,y=3x-6=3,
∴方程3x-y=6的一组正整数解为$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$.
(2)∵12的因数有:1、2、3、4、6、12,
∴使$\frac{12}{x-3}$为自然数的x值有:4、5、6、7、9、15.
故答案为:B.
(3)设笔记本买了x本,钢笔买了y支,
根据题意得:3x+5y=48,
∴x=16-$\frac{5}{3}$y.
∵x、y均为正整数,
∴y为3的倍数.
当y=3时,x=11;
当y=6时,x=6;
当y=9时,x=1.
∴共有三种购买方案,方案一:购买11个笔记本、3支钢笔;方案二:购买6个笔记本、6支钢笔;方案三:购买1个笔记本、9支钢笔.
点评 本题考查了二元一次方程的应用,解题的关键是:(1)代入x=3求出y值;(2)根据12因数的个数找出x值的个数;(3)由x、y均为正整数解二元一次方程3x+5y=48.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
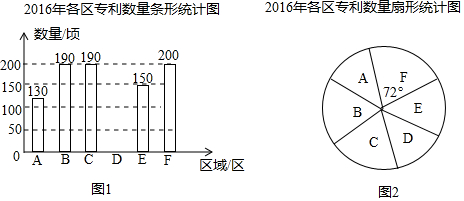
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
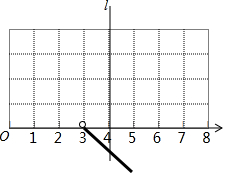 如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.
如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上几个关于直线l对称的点,如果小球起始时位于(1,0)处,仍按原来方向击球,请你画出这时小球运动的轨迹.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m.设AD的长为x m,菜园ABCD的面积为y m2.则函数y关于自变量x的函数关系式是y=(30-2x)x,x的取值范围是6≤x<15.
如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m.设AD的长为x m,菜园ABCD的面积为y m2.则函数y关于自变量x的函数关系式是y=(30-2x)x,x的取值范围是6≤x<15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com