试题分析:(1)可直接求出角的度数;(2)要考虑到在∠COD内部和∠COD外部两种情况;(3)要分几种情况加以讨论.
试题解析:(1)∠BOD=90°-∠AOC-∠AOB=90°-20°-30°=40°.(2)如图

∠AOC=90°-∠BOD-∠AOB ∠AOC= 90°+∠BOD-∠AOB
=90°-20°-30°=40° = 90°+20°-30°=80°
所以转动了40°或转动了80°;
(3)①OB边在∠COD内部或与OD重合,如图:关系式为:∠AOC+∠BOD=60°,理由是

∠AOC+∠BOD=90°-∠AOB=90°-30°=60°;
②OA边在∠COD内部或与OD重合,OB边在∠COD外部,如图:关系式为∠AOC-∠BOD=60°,理由因为∠AOC=90°-∠AOD,∠BOD=30°-∠AOD,
所以∠AOC-∠BOD=(90°-∠AOD)-(30°-∠AOD)=90°-∠AOD-30°+∠AOD=60°;

③OA、OB都在∠COD外部,如图:此时关系式为∠AOC-∠BOD=60°理由为

因为∠AOC=90°+∠AOD,∠BOD=30°+∠AOD,
所以∠AOC-∠BOD=(90°+∠AOD)-(30°+∠AOD)=90°+∠AOD-30°-∠AOD=60°
综合上述:∠AOC与∠BOD的关系为:∠AOC+∠BOD=60°或∠AOC-∠BOD=60°.














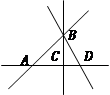
 BC B.AN=
BC B.AN=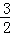 AB C.BM:BN=1:2 D.AM=
AB C.BM:BN=1:2 D.AM= BC
BC