
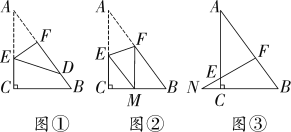
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上的点,连接EF.
(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,AE的长为 ;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE=![]() ,则
,则![]() = .
= .
【答案】(1)![]() ;(2)①四边形AEMF是菱形,见解析;②EF
;(2)①四边形AEMF是菱形,见解析;②EF![]() ;(3)
;(3)![]()
【解析】
(1)先利用折叠的性质得到EF⊥AB,△AEF≌△DEF,则S△AEF=S△DEF,则易得S△ABC=4S△AEF,再证明Rt△AEF∽Rt△ABC,然后根据相似三角形的性质得到![]() ,再利用勾股定理求出AB即可得到AE的长;
,再利用勾股定理求出AB即可得到AE的长;
(2)①邻边相等的平行四边形即为菱形,即可证明AEMF为菱形;
②连结AM交EF于点O,如图②,设AE=x,则EM=x,CE=4-x,先证明△CME∽△CBA得到![]() ,解出x后计算出CM=
,解出x后计算出CM=![]() ,再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
,再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
(3)如图③,作FH⊥BC于H,先证明△NCE∽△NFH,利用相似比得到FH:NH=4:7,设FH=4x,NH=7x,则CH=7x-1,BH=3-(7x-1)=4-7x,再证明△BFH∽△BAC,利用相似比可计算出x=![]() ,则可计算出FH和BH,接着利用勾股定理计算出BF,从而得到AF的长,于是可计算出
,则可计算出FH和BH,接着利用勾股定理计算出BF,从而得到AF的长,于是可计算出![]() 的值.
的值.
(1)如图①,
∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF=S△DEF,
∵S四边形ECBF=3S△EDF,
∴S△ABC=4S△AEF,
在Rt△ABC中,
∵∠ACB=90°,AC=4,BC=3,
∴AB=5,
∵∠EAF=∠BAC
∴Rt△AEF∽Rt△ABC,
∴![]() ,即
,即![]() S
S
AE=![]()
(2)①四边形AEMF是菱形,理由如下:
如图②:∵折叠后点A落在BC边上的点M处,
∴∠CAB=∠EMF,AE=ME,
又∵MF∥CA,
∴∠CEM=∠EMF.
∴∠CAB=∠CEM.
∴EM∥AF.
∴四边形AEMF是平形四边形.
又∵AE=ME,
∴四边形AEMF是菱形
②连接AM、AM与EF交于点O,如图②,
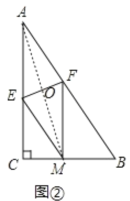
设AE=x,则AE=ME=x,EC=4-x.
∵∠
∴Rt△ECM∽Rt△ACB
∴![]()
即![]()
解得x=![]() ,CM=
,CM=![]()
在Rt△ACM中,
AM=![]()
∵S菱形AEMF=![]()
∴EF=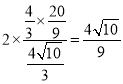
(3)如图③,作FH⊥BC于H
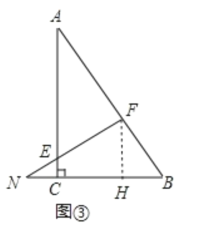
∵EC∥FH,
∴△NCE∽△NFH,
∴CN:NH=CE:FH,即1:NH=![]() :FH,
:FH,
∴FH:NH=4:7,
设FH=4x,NH=7x,
则CH=7x1,BH=3(7x1)=47x,
∵FH∥AC,
∴△BFH∽△BAC,
∴BH:BC=FH:AC,即(47x):3=4x:4,
解得x=![]() ,
,
∴FH=4x=![]() ,BH=47x=
,BH=47x=![]()
在Rt△BFH中,BF=![]()
∴AF=ABBF=52=3,
∴![]()


科目:初中数学 来源: 题型:
【题目】某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
(参考数据:sin48°≈![]() ,tan48°≈
,tan48°≈![]() ,sin64°≈
,sin64°≈![]() ,tan64°≈2)
,tan64°≈2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )
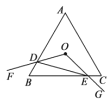
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,CD为⊙O的切线,点C是切点.
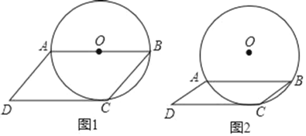
(1)如图1,若AB为⊙O直径,求四边形ABCD各内角的度数;
(2)如图2,若AB为弦,⊙O的半径为3cm,当BC=2cm时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=7,BC=4,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E、F,则EF=__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是边AD上一点(不与点A重合),连结BE,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连结BP、EQ.求证:四边形BPEQ是菱形.
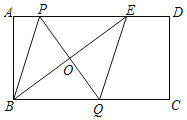
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
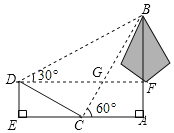
A.20![]() B.30C.30
B.30C.30![]() D.40
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
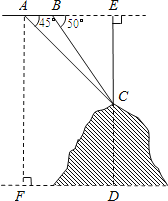
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com