
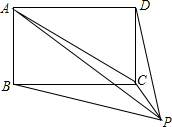
 如图,P为矩形ABCD外一点,猜想S△PBC、S△PAC、S△PCD之间的数量关系,并证明.
如图,P为矩形ABCD外一点,猜想S△PBC、S△PAC、S△PCD之间的数量关系,并证明. 分析 首先过点P作PE⊥AD,分别交AD、BC的延长线于E、F两点,由P为矩形ABCD外一点,可得AD=BC,PF⊥BC,然后由三角形面积可得:S△PAC+S△PCD=S△PAD-S△CAD=$\frac{1}{2}$AD•PE-$\frac{1}{2}$AD•EF=$\frac{1}{2}$AD•(PE-EF)=$\frac{1}{2}$AD•PF,S△PBC=$\frac{1}{2}$BC•PF,则可求得答案.
解答 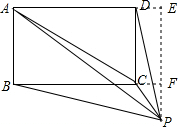 解:S△PBC=S△PAC+S△PCD.
解:S△PBC=S△PAC+S△PCD.
理由:过点P作PE⊥AD,分别交AD、BC的延长线于E、F两点.
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴PF⊥BC,
∵S△PAC+S△PCD=S△PAD-S△CAD=$\frac{1}{2}$AD•PE-$\frac{1}{2}$AD•EF=$\frac{1}{2}$AD•(PE-EF)=$\frac{1}{2}$AD•PF,S△PBC=$\frac{1}{2}$BC•PF,
∴S△PBC=S△PAC+S△PCD.
点评 此题考查了矩形的性质以及三角形的面积.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.
已知A(-5,0),B($\sqrt{5}$,0),P点为直线y=$\frac{1}{3}x+\frac{5}{3}$上的一个动点,P点的横坐标为a,若∠APB为钝角,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com