
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
【答案】(1)证明见详解(2)当![]() 时,四边形
时,四边形![]() 能够成为菱形;理由见详解(3)当
能够成为菱形;理由见详解(3)当![]() 或
或![]() 时,
时,![]() 为直角三角形;理由见详解
为直角三角形;理由见详解
【解析】
(1)根据时间和速度表示出![]() ,
,![]() ,再利用
,再利用![]() 角所对的直角边等于斜边的一半求得
角所对的直角边等于斜边的一半求得![]() ,则可得
,则可得![]() ,然后根据平行线的判定得到
,然后根据平行线的判定得到![]() ,即可得证结论;
,即可得证结论;
(2)由(1)的结论可得四边形![]() 是平行四边形,若
是平行四边形,若![]() 为菱形,则必有邻边相等,则
为菱形,则必有邻边相等,则![]() ,列出关于
,列出关于![]() 的方程求解即可;
的方程求解即可;
(3)当![]() 为直角三角形时,分三种情况分别找等量关系列方程求解即可.
为直角三角形时,分三种情况分别找等量关系列方程求解即可.
解:(1)根据题意得:![]() ,
,![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴四边形![]() 是平行四边形;
是平行四边形;
(2)结论:四边形![]() 能够成为菱形
能够成为菱形
理由:由(1)可知四边形![]() 是平行四边形
是平行四边形
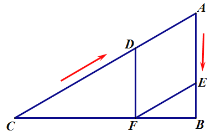
若![]() 为菱形,则
为菱形,则![]() ,如图:
,如图:
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴当![]() 时,四边形
时,四边形![]() 能够成为菱形;
能够成为菱形;
(3)①当![]() 时,如图:
时,如图:
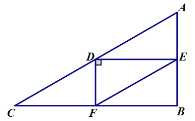
∵![]() ,
,![]()
∴四边形![]() 为矩形
为矩形
∴![]()
∵由(1)可知四边形![]() 是平行四边形
是平行四边形
∴![]()
∵由(1)可知![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
②当![]() 时,如图:
时,如图:
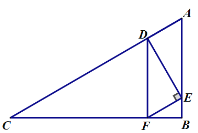
∵由(1)可知四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ;
;
③当![]() 时,不成立;
时,不成立;
∴综上所述,当![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.


科目:初中数学 来源: 题型:
【题目】一个口袋中装有3个白球、5个红球,这些球除了颜色外完全相同,充分摇匀后随机摸出一球,
(1)求摸出白球概率是多少?
(2)在第一次摸出白球后,如果将这个白球放回,再摸出一球,求两次摸出的都是白球的概率是多少?(用树状图或列表分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
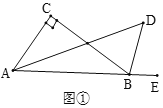
【题目】(1)如图①,在△ABC中,∠C=90°,∠BAC的平分线与外角∠CBE的平分线相交于点D,求∠D的度数.
(2)如图②,将(1)中的条件“![]() ”改为
”改为![]() ,其它条件不变,请直接写出
,其它条件不变,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com