
 O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB.
O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB.分析 (1)根据角平分线的定义得到∠OBC+∠OCB的值,再利用三角形的内角和定理求出∠BOC的值;
(2)根据角平分线的定义和三角形的内角和定理求出∠OBC+∠OCB的值,再利用三角形的内角和定理求出∠BOC的度数;
(3)根据角平分线的定义和三角形的内角和定理求出∠OBC+∠OCB的值,再利用三角形的内角和定理求出∠BOC的值.
解答 解:(1)∵BO,CO分别平分∠ABC,∠ACB,∠ABC=80°,∠ACB=60°,
∴∠OBC=$\frac{1}{2}$∠ABC=40°,∠OCB=$\frac{1}{2}$∠ACB=30°,
∴∠BOC=180°-40°-30°=110°;
(2)∵∠A=40°,∴∠ABC+∠ACB=180°-40°=140°,
∴∠OBC+∠OCB=70°,
∴∠BOC=180°-70°=110°;
(3)∵∠A=α,∴∠ABC+∠ACB=180°-α,
∴∠OBC+∠OCB=$\frac{1}{2}$(180°-α),
∴∠BOC=180°-$\frac{1}{2}$(180°-α)=90°+$\frac{1}{2}α$.
点评 本题考查的是三角形的内角和定理和角平分线的定义,同时考查了整体思想的应用,是一道常见的难题,解答时,需要学生认真审题,熟练运用性质和定理.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
 已知如图,AE∥x轴,OA平分∠EOC,点A(2,2),点B(0,-2),AB交x轴于点D,AC⊥AB交x轴于点C,且AB=AC.
已知如图,AE∥x轴,OA平分∠EOC,点A(2,2),点B(0,-2),AB交x轴于点D,AC⊥AB交x轴于点C,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示为某大厦的示意图其中裙楼共有10层,现测得DF的高为55米,吴莉在D处测得地面上点B的俯角α为30°,点D到AM的距离DE为60米,从地面上的点B沿BM方向走到点C处,测得BC=50米,大厦顶尖A的仰角β为65°,请根据以上测量数据计算大厦的高AM.(结果精确到0.1米,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.143,$\sqrt{3}$≈1.732)
如图所示为某大厦的示意图其中裙楼共有10层,现测得DF的高为55米,吴莉在D处测得地面上点B的俯角α为30°,点D到AM的距离DE为60米,从地面上的点B沿BM方向走到点C处,测得BC=50米,大厦顶尖A的仰角β为65°,请根据以上测量数据计算大厦的高AM.(结果精确到0.1米,参考数据:sin65°≈0.906,cos65°≈0.423,tan65°≈2.143,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
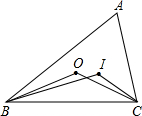 如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )
如图,点I和O分别是△ABC的内心和外心,则∠BIC与∠BOC的关系为( )| A. | ∠BIC=∠BOC | B. | ∠BIC≠∠BOC | ||
| C. | 2∠BIC-$\frac{1}{2}$∠BOC=180° | D. | 2∠BOC-$\frac{1}{2}$∠BIC=180° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com