
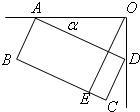
 7、如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为55cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
7、如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为55cm,若AO=100cm,则墙角O到前沿BC的距离OE是( ) 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
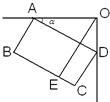 16、如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是
16、如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是查看答案和解析>>
科目:初中数学 来源: 题型:
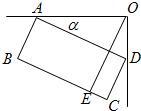 19、如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=a,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
19、如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=a,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )查看答案和解析>>
科目:初中数学 来源: 题型:
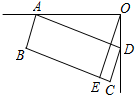 (2012•黄陂区模拟)如图是一台54英寸的大背投彩电放置在墙角的俯视图(其中ABCD是矩形).设∠ADO=α,彩电后背AD与前沿BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
(2012•黄陂区模拟)如图是一台54英寸的大背投彩电放置在墙角的俯视图(其中ABCD是矩形).设∠ADO=α,彩电后背AD与前沿BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )查看答案和解析>>
科目:初中数学 来源:2009年浙江省宁波市十九中中考数学模拟考试四校联考试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com