
如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点P沿AB边从A向B以2 cm/s的速度移动;点Q沿DA边从D向A以1 cm/s的速度移动.如果P,Q同时出发,用t(s)表示移动时间(0≤t≤6),那么:
(1)当t为何值时,△QAP为 等
等 腰直角三角形?
腰直角三角形?
(2)求四边形QAPC的面积,你有什么发现?
(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABC相似?
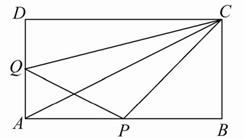
【解析】(1)对于任意时刻的t有:AP=2t,DQ=t,
AQ=6-t,
当AQ=AP时,△QAP为等腰直角三角形,
即6-t=2t,∴t=2,
∴当t=2时,△QAP为等腰直角三角形.
(2)在△AQC中,AQ=6-t,AQ边上的高CD=12,
∴S△AQC=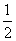 (6-t)×12=36-6t,
(6-t)×12=36-6t,
在△APC中,AP=2t,AP边上 的高CB=6,
的高CB=6,
∴S△APC=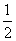 ×2t×6=6t.
×2t×6=6t.
∴四边形QAPC的面积
S四边形Q APC=S△AQC+S△A
APC=S△AQC+S△A PC
PC
=36-6t+6t=36(cm2),
所以,经计算发现:点P,Q在运动的过程中,四边形QAPC的面积保持不变.
(3)根据题意,应分两种情况来研究:
①当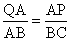 时,△QAP∽△ABC,
时,△QAP∽△ABC,
则有 ,求得t=1.2(s).
,求得t=1.2(s).
②当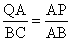 时,△PAQ∽△ABC,
时,△PAQ∽△ABC,
则有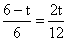 ,求得t=3(s)
,求得t=3(s)
∴当t=1.2或3时,以点A,P,Q为顶点的三角形与△ABC相似.


科目:初中数学 来源: 题型:
小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字3、4、5,现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.如果和为奇数,则小明胜;和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为8的概率;
(2)你认为这个游戏对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
定义:如果一元二次方程 满足
满足 ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是( )
A.a=c B.a=b C.b=c D.a=b=c
查看答案和解析>>
科目:初中数学 来源: 题型:
为支援四川地震灾区,中央电视台于5月18日晚举办了《爱的奉献》赈灾晚会,晚会现场捐款达1 514 000 000元.1 514 000 000保留两个有效数字的近似数是( )
A.15×106  B.15×108 C.1.5×109 D.1.5×1010
B.15×108 C.1.5×109 D.1.5×1010
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com