Question

学校组织师生共360人参加游园活动，有载客量分别为45人、30人两种客车可供租用，要求每辆车必须满载，则师生一次性全部到达公园的租车方案有

1. A.
   3种
2. B.
   4种
3. C.
   5种
4. D.
   6种

Answer 1

C
分析：设租用载客量45人的客车x辆，租用载客量30人的客车y辆，根据两种车的载客总人数360人建立方程求出其解即可．
解答：设租用载客量45人的客车x辆，租用载客量30人的客车y辆，由题意，得
45x+30y=360，
x=，
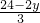
∵x≥0，y≥0．x、y为非负整数，
∴24-2y≥0，
y≤12，
∵24-2y是3的倍数，
∴24-2y=0，3，6，9，12，15，18，21，24，
∴y=12，10.5（舍去），9，7.5（舍去），6，4.5（舍去），3，1.5，0，
∴x=0，2，4，6，8
∴共有5种租车方案：
方案1：租用载客45人的客车0辆，租用载客量30人的客车12辆，
方案2：租用载客45人的客车2辆，租用载客量30人的客车9辆，
方案1：租用载客45人的客车4辆，租用载客量30人的客车6辆，
方案1：租用载客45人的客车6辆，租用载客量30人的客车3辆，
方案1：租用载客45人的客车8辆，租用载客量30人的客车0辆，
故选C．
点评：本题考查了列二元一次不定方程解实际问题的运用，不定方程的解法的运用，在解答时根据条件建立方程是关键，根据未知数的隐含条件求解是难点．
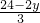