
【题目】火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A,B两种型号的车厢将这批货物运至北京,已知每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨和乙种货物35吨可装满一节B型车厢,按此要求安排A,B两种车厢的节数,共有哪几种方案?请你设计出所有方案,并说明哪种方案的运费最少.
【答案】运送方案有三种:
方案一:A型车厢28节,B型车厢22节;
方案二:A型车厢29节,B型车厢21节;
方案三:A型车厢30节,B型车厢20节.
方案三运费最少.
【解析】
A型货厢装甲种货物吨数+B型货厢装甲种货物吨数≥1530;A型货厢装乙种货物吨数+B型货厢装乙种货物吨数≥1150,把相关数值代入可得一种货厢节数的范围,进而求得总运费的等量关系,根据函数的增减性可得最少运费方案及最少运费.
解:设A型车厢为x节,则B型车厢为(50-x)节,
根据题意得![]() ,
,
解得28≤x≤30.
因为x为整数,所以x取28,29,30.
因此运送方案有三种:
方案一:A型车厢28节,B型车厢22节;
方案二:A型车厢29节,B型车厢21节;
方案三:A型车厢30节,B型车厢20节.
设运费为y万元,则y=0.5x+0.8(50-x)=40-0.3x,
当x=28时,y=31.6;当x=29时,y=31.3;当x=30时,y=31.
因此,选方案三,即A型车厢30节,B型车厢20节时运费最少.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】现有足够多的正方形和长方形的卡片,如图1所示,请运用拼图的方法,选取相应种类和数量的卡片,按要求回答下列问题.
(1)根据图2,利用面积的不同表示方法,写出一个代数恒等式:______________________;
(2)若要拼成一个长为![]() ,宽为
,宽为![]() 的长方形,则需要甲卡片____张,乙卡片____张,丙卡片____张;
的长方形,则需要甲卡片____张,乙卡片____张,丙卡片____张;

(3)请用画图结合文字说明的方式来解释:![]() ≠
≠![]() (
(![]() ≠0,
≠0,![]() ≠0).
≠0).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论错误的是( )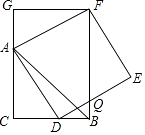
A.AC=FG
B.S△FAB:S四边形CBFG=1:2
C.AD2=FQAC
D.∠ADC=∠ABF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14
B.y=x2-8x+14
C.y=x2+4x+3
D.y=x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
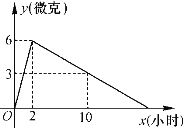
【题目】某医院研发了一种新药,试验药效时发现,如果成人按规定剂量服用,那么服药2小时后,血液中含药量最高,达每毫升6微克,接着逐渐衰减,10小时后血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后:
(1)服药后几小时血液中含药量最高?达到每毫升血液中含药多少微克?
(2)在服药几个小时后,血液中的含药量逐渐升高?在几小时后,血液中的含药量逐渐衰减?
(3)服药后10小时时,血液中含药量是多少微克?
(4)服药几小时后即已无效?
查看答案和解析>>
科目:初中数学 来源: 题型:
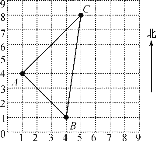
【题目】如图所示是某学校的平面图的一部分,其中A代表音乐楼,B代表实验楼,C代表图书馆,正方形网格中每个小正方形的边长为1,试结合图形回答下列问题:
(1)用(1,4)表示音乐楼A的位置,那么实验楼B和图书馆C的位置如何表示?
(2)三座楼房之间修三条路AC,AB,BC,且已知这三条路的长度存在下列关系:AC2+AB2=BC2.量得B到A的距离为3![]() ,若记东偏北方向为“+”,东偏南方向为“-”,则B点相对于A点的位置记作(-45°,3
,若记东偏北方向为“+”,东偏南方向为“-”,则B点相对于A点的位置记作(-45°,3![]() ).那么,C点相对于A点的位置可如何表示?
).那么,C点相对于A点的位置可如何表示?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com