
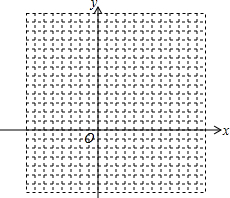
 已知:(-4,-1),(-2,0),(-1,4),(0,-5),(0,0),(0,1),(1,4),(2,2),(3,0),(4,1),(4,3),(6,4).将这12个点按要求进行不同的分类:
已知:(-4,-1),(-2,0),(-1,4),(0,-5),(0,0),(0,1),(1,4),(2,2),(3,0),(4,1),(4,3),(6,4).将这12个点按要求进行不同的分类:分析 (1)根据点在x轴上,纵坐标均为0,点在y轴上,横坐标均为0,即可解答;
(2)计算横、纵坐标的积即可解答.
解答 解:(1)在坐标轴上的点有:(-2,0)、(0,-5),(0,0),(0,1),(3,0),
不在坐标轴上的点有:(-4,-1)、(-1,4)、(1,4),(2,2),(4,1),(4,3),(6,4);
(2)横、纵坐标的积等于4的有:(-4,-1)、(1,4),(2,2),(4,1),
横、纵坐标的积不等于4的有:(-2,0)、(-1,4)、(0,-5),(0,0),(0,1),(3,0),(4,3),(6,4).
点评 本题考查了坐标与图形性质,解决本题的关键是明确坐标轴上点的特点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 随着抛掷次数的增加,正面向上的频率越来越小 | |
| B. | 当抛掷的次数n很大时,正面向上的次数一定为$\frac{n}{2}$ | |
| C. | 不同次数的试验,正面向上的频率可能会不相同 | |
| D. | 连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率小于$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
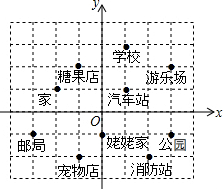 下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.
下图中标明了小红家附近的一些地方,建立平面直角坐标系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
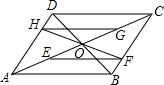 如图,?ABCD的两条对角线AC、BD相交于点O,E、G分别是OA、OC的中点,过点O作任一条直线交AD于点H,交BC于点F,猜想EF与HG的关系,并证明你的猜想.
如图,?ABCD的两条对角线AC、BD相交于点O,E、G分别是OA、OC的中点,过点O作任一条直线交AD于点H,交BC于点F,猜想EF与HG的关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
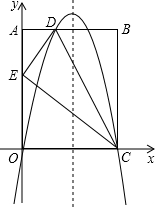 如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.
如图,在平面直角坐标系中,已知矩形OABC的三个顶点A(0,10),B(8,10),C(8,0),过O、C两点的抛物线y=ax2+bx+c与线段AB交于点D,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com