
分析 根据在Rt△ABC中,∠C=90°,a=$\frac{1}{3}$,c=$\frac{\sqrt{2}}{3}$,可以求得b的值和sinA的值,从而可以求得∠A的度数,进而求得∠B的度数.
解答 解:∵在Rt△ABC中,∠C=90°,a=$\frac{1}{3}$,c=$\frac{\sqrt{2}}{3}$,
∴b=$\sqrt{{c}^{2}-{a}^{2}}=\sqrt{(\frac{\sqrt{2}}{3})^{2}-(\frac{1}{3})^{2}}$=$\frac{1}{3}$,sinA=$\frac{a}{c}=\frac{\frac{1}{3}}{\frac{\sqrt{2}}{3}}=\frac{\sqrt{2}}{2}$,
∴∠A=45°,
∴∠B=90°-∠A=45°,
故答案为:$\frac{1}{3}$,45°,45°.
点评 本题考查解直角三角形,解题的关键是明确题意,找出所求问题需要的条件.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
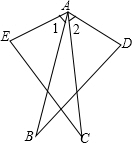 如图,已知AB=AC,∠1=∠2,∠B=∠C,则BD=CE.请说明理由:
如图,已知AB=AC,∠1=∠2,∠B=∠C,则BD=CE.请说明理由:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
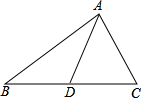 如图,△ABC中,点D在BC上,连结AD.
如图,△ABC中,点D在BC上,连结AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.
如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且$\widehat{DE}$=$\widehat{BE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
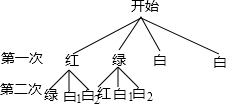 一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com