
分析 (1)设购买一个A品牌的篮球需x元,购买一个B品牌的篮球需y元,根据“购买一个B品牌蓝球比购买一个A品牌蓝球多花30元,购买2个A品牌篮球和3个B品牌篮球共需340元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设此次购买B品牌篮球m个,则购买A品牌篮球(50-m)个,根据总价=单价×购买数量结合总费用不超过3260元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,取其内的最大值即可;
(3)设购买50个篮球所需总费用为w元,根据总价=单价×购买数量,即可得出w关于m的函数关系式,再利用一次函数的性质即可解决最值问题.
解答 解:(1)设购买一个A品牌的篮球需x元,购买一个B品牌的篮球需y元,
根据题意得:$\left\{\begin{array}{l}{x+30=y}\\{2x+3y=340}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=80}\end{array}\right.$.
答:购买一个A品牌的篮球需50元,购买一个B品牌的篮球需80元.
(2)设此次购买B品牌篮球m个,则购买A品牌篮球(50-m)个,
根据题意得:50×(1+8%)(50-m)+80×0.9m≤3260,
解得:m≤31$\frac{1}{9}$.
∵m为正整数,
∴m≤31.
答:该中学此次最多可购买31个B品牌蓝球.
(3)设购买50个篮球所需总费用为w元,
根据题意得:w=50×(1+8%)(50-m)+80×0.9m=18m+2700.
∵购买A品牌篮球的数量不超过22个,
∴50-m≤22,
∴m≥28.
又∵m≤31,
∴28≤m≤31.
∵在w=18m+2700中,k=18>0,
∴当m=28时,w取最小值,最小值为3204.
答:当购买A品牌篮球22个、B品牌篮球28个时,总费用最低,最低费用为3204元.
点评 本题考查了二元一次方程组的应用、一元一次不等式的应用、一次函数的应用以及一次函数的最值,解题的关键是:(1)找准等量关系,列出关于x、y的二元一次方程组;(2)根据总价=单价×购买数量结合总费用不超过3260元,列出关于m的一元一次不等式;(3)根据总价=单价×购买数量,找出w关于m的函数关系式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 大型造型树木 | 小型景观乔木 | ||||
| 投资金额x(万元) | x | 5 | x | 2 | 4 |
| 市场利润y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.4 | 3.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
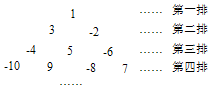 将整数1,-2,3,-4,5,-6,…按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数2017的有序实数对是(64,64).
将整数1,-2,3,-4,5,-6,…按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数2017的有序实数对是(64,64).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com