
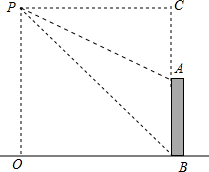
 直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和60°,求飞机的高度PO.
直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和60°,求飞机的高度PO. 分析 过P作PC⊥AB交BA的延长线于C,连接PA,PB,于是得到∠PBO=∠CPB=60°,∠CPA=30°,求得∠APB=30°,根据余角的定义得到∠ABP=90°-60°=30°,求出∠ABP=∠APB,根据等腰三角形的判定得到AP=AB=200,在Rt△APC中,根据含30°角的直角三角形的性质得到AC=$\frac{1}{2}$AP=100,即可得到结论.
解答 解:过P作PC⊥AB交BA的延长线于C,连接PA,PB,
则∠PBO=∠CPB=60°,∠CPA=30°,
∴∠APB=30°,
∵∠ABP=90°-60°=30°,
∴∠ABP=∠APB,
∴AP=AB=200,
在Rt△APC中,AC=$\frac{1}{2}$AP=100,
∴PO=AC+AB=300米.
答:飞机的高度PO为300米.
点评 本题考查了解直角三角形的知识,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}>-|-2|>-{2^2}>{(-2)^3}$ | B. | (-2)3>-22>-|-2|>-$\frac{1}{2}$ | ||
| C. | -|-2|>-$\frac{1}{2}>-{2^2}>{(-2)^3}$ | D. | -22>(-2)3>-$\frac{1}{2}$>-|-2| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 国家 | 中国 | 美国 | 俄罗斯 | 英国 | 德国 | 澳大利亚 | 其他 |
| 金牌数/枚 | 51 | 36 | 23 | 19 | 16 | 14 | 143 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com