在等号成立时.等式右边填上适当的符号:$\frac{y-x}{{{x^2}-{y^2}}}$=-$\frac{1}{x+y}$．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

16．在等号成立时，等式右边填上适当的符号：$\frac{y-x}{{{x^2}-{y^2}}}$=-$\frac{1}{x+y}$．

分析由$\frac{y-x}{{{x^2}-{y^2}}}$=$\frac{-（x-y）}{（x+y）（x-y）}$，约分即可得出答案．

解答解：∵$\frac{y-x}{{{x^2}-{y^2}}}$=$\frac{-（x-y）}{（x+y）（x-y）}$=-$\frac{1}{x+y}$，
故答案为：-．

点评本题主要考查分式的值，熟练掌握分式的基本性质以化简分式是解题的关键．

练习册系列答案

小学毕业升学复习必做的18套试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

12．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利50元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价10元，商场平均每天可多售出20件．
（1）若商场平均每天要盈利1600元，每件衬衫应降价多少元？
（2）怎样定价能获得最大利润，最大利润是多少？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．某同学解关于x的方程$\frac{2x-1}{3}$=$\frac{x+a}{3}$-1，在去分母时，右边的-1没有乘3，因此求得方程的解是x=3，试求a的值及原方程的解．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

4．已知AB、BC是⊙O的两条弦，AB=$\frac{\sqrt{6}}{2}$AC，∠AOB=120°，则∠CAB的度数是15°或75°．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

11．

已知正方形ABCD的边长为1，AC为对角线，作DO₁⊥AC，O₁为垂足，作O₁O₂⊥AD，O₂为垂足，作O₂O₃⊥AO₁，O₃为垂足，作O₃O₄⊥O₁O₂，O₄为垂足，…，请你仔细观察图，然后计算：$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…=1．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

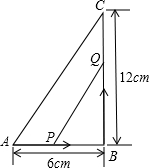如图，在△ABC中，∠B=90°，点P从点B开始沿BA边向点A以1cm/s的速度移动，Q从点C开始沿CB边向B点以2cm/s的速度移动．如果点P、Q分别从B、C同时出发．
（1）求几秒钟后，△PBQ的面积等于8cm²？
（2）求几秒钟后，PQ的长度等于4$\sqrt{2}$cm？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

8．

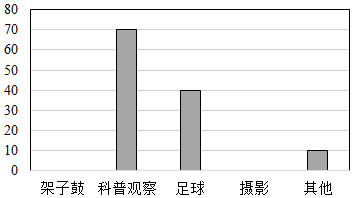为了深化我省义务教育课程改革，某校积极开展本校课程建设，计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团，要求每个学生都自主选择其中一个社团．为此，随机调查了本校七、八、九年级部分学生选择社团的意向，并将调查结果绘制成如图统计表（不完整）：
某校被调查学生选择社团意向统计表

选择意向	架子鼓	科普观察	足球	摄影	其他
所占百分比	30%	a	b	10%	c

根据统计图表中的信息，解答下列问题：
（1）求架子鼓和摄影社团的人数及a，b的值；
（2）将条形统计图补充完整；
（3）若该校共有1200名学生，试估计全校选择“科普观察”社团的学生人数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

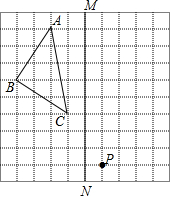如图，在正方形网格上的一个△ABC．（其中点A、B、C均在网格上）
（1）作△ABC关于直线MN的轴对称图形；
（2）以P点为一个顶点作一个与△ABC全等的三角形（规定点P与点B对应，另两顶点都在图中网格交点处）．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

6．若关于x的一元二次方程为ax²+bx+c=0的两根之和为3，则关于x的方程a（x+1）²+b（x+1）+c=0的两根之和为1．

查看答案和解析>>

同步练习册答案