
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
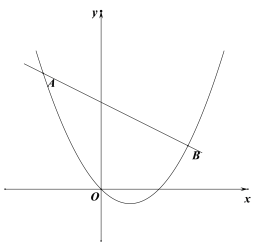
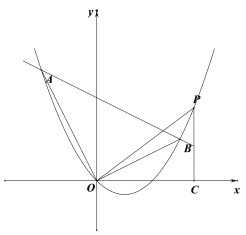
(1)求抛物线的解析式.
(2)在直线![]() 下方的抛物线上求点
下方的抛物线上求点![]() ,求
,求![]() 的面积等于20.
的面积等于20.
(3)若![]() 在抛物线上,作
在抛物线上,作![]() 轴于点
轴于点![]() ,若
,若![]() 和
和![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)(-2,3)或(4,0);(3)
;(2)(-2,3)或(4,0);(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)根据抛物线![]() 相交于
相交于![]() ,
,![]() 两点,用待定系数法列方程组求解即可得到答案;
两点,用待定系数法列方程组求解即可得到答案;
(2)作PD//y轴,交AB于点D,设![]() ,则
,则![]() ,把BD的长度表示出来,再根据三角形的面积公式列等式,求解即可得到答案;
,把BD的长度表示出来,再根据三角形的面积公式列等式,求解即可得到答案;
(3)先用勾股定理的逆定理证明∠AOB=![]() ,再分CPO∽OBA 或者CPO∽OBA两种情况讨论即可得到答案;
,再分CPO∽OBA 或者CPO∽OBA两种情况讨论即可得到答案;
解:(1)∵抛物线![]() 相交于
相交于![]() ,
,![]() 两点,
两点,
将A(-4,8),B(6,3)代入![]() ,联立得:
,联立得:
![]() ,
,
解得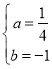 ,
,
所求的抛物线的解析式为:![]() .
.
(2)如图,作PD//y轴,交AB于点D,
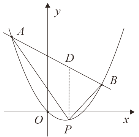
设![]() ,则
,则![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
故所求的点P为(-2,3)或(4,0).
(3)设![]() ,如图,
,如图,
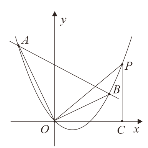
根据勾股定理得到:![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴∠AOB=![]() (勾股定理的逆定理),
(勾股定理的逆定理),
∠AOB=∠PCO,
当![]() 时,CPO∽OBA .
时,CPO∽OBA .
即: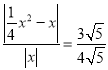 ,
,
整理得:![]() ,
,
解方程:![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时P点坐标为
,此时P点坐标为![]() ;
;
解方程:![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时P点坐标为
,此时P点坐标为![]() .
.
当![]() 时,CPO∽OBA .
时,CPO∽OBA .
解即: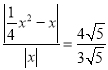 ,
,
整理得:![]() ,
,
解方程:![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时P点坐标为
,此时P点坐标为![]() .
.
解方程:![]() ,得
,得![]() (舍去),
(舍去),![]() ,此时P点坐标
,此时P点坐标![]() .
.
综上所述,所求点P的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)(发现证明)
如图1,在正方形ABCD中,点E,F分别是BC,CD边上的动点,且∠EAF=45°,求证:EF=DF+BE.

小明发现,当把△ABE绕点A顺时针旋转90°至△ADG,使AB与AD重合时能够证明,请你给出证明过程.
(2)(类比引申)①如图2,在正方形ABCD中,如果点E,F分别是CB,DC延长线上的动点,且∠EAF=45°,则(1)中的结论还成立吗?请写出证明过程.
②如图3,如果点E,F分别是BC,CD延长线上的动点,且∠EAF=45°,则EF,BE,DF之间的数量关系是 (不要求证明)
(3)(联想拓展)如图1,若正方形ABCD的边长为6,AE=3![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
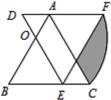
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=ax2+bx+c(a≠0)的顶点坐标A(﹣1,3),与x轴的一个交点B(﹣4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a﹣b=0;②abc<0;③抛物线与x轴的另一个交点坐标是(3,0);④方程ax2+bx+c﹣3=0有两个相等的实数根;⑤当﹣4<x<﹣1时,则y2<y1.
其中正确的是( )

A. ①②③ B. ①③⑤ C. ①④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上一点(不与点A、B重合),D是![]() 的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.
的中点,DE⊥AB于点E,过点C作半圆O的切线,交ED的延长线于点F.
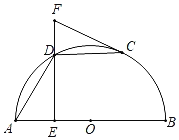
(1)求证:∠FCD=∠ADE;
(2)填空:
①当∠FCD的度数为 时,四边形OADC是菱形;
②若AB=2![]() ,当CF∥AB时,DF的长为 .
,当CF∥AB时,DF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G网络,是最新一代蜂窝移动通信技术,其数据传输速率远高于以前的蜂窝网络,最高可达10Gbit/s,比4G快100倍.5G手机也成为生活、工作不可缺少的移动设备,某电商公司销售两种5G手机,已知售出5部A型手机,3部B型手机的销售额为51000元;售出3部A型手机,2部B型手机的销售额为31500元.
(1)求A型手机和B型手机的售价分别是多少元;
(2)该电商公司在3月实行“满减促销”活动,活动方案为:单部手机满3000元减500元,满5000元减1500元(每部手机只能参加最高满减活动),结果3月A型手机的销量是B型手机的![]() ,4月该电商公司加大促销活动力度,每部A型手机按照3月满减后的售价再降
,4月该电商公司加大促销活动力度,每部A型手机按照3月满减后的售价再降![]() a%,销量比3月增加2a%;每部B型手机按照满减后的售价再降a%,销量比3月销量增加
a%,销量比3月增加2a%;每部B型手机按照满减后的售价再降a%,销量比3月销量增加![]() a%,结果4月的销售总额比3月的销售总额多
a%,结果4月的销售总额比3月的销售总额多![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在 A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( ).(参考数据sin53°≈0.80,cos53°≈0.60)
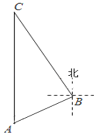
A.12千米B.(3+4![]() )千米C.(3+5
)千米C.(3+5![]() )千米D.(12﹣4
)千米D.(12﹣4![]() )千米
)千米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com