
 ,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
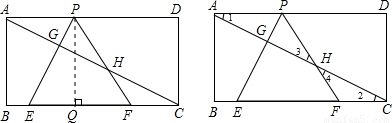 解:(1)过P作PQ⊥BC于Q
解:(1)过P作PQ⊥BC于Q
 ∴PF=2∴△PEF的边长为2. (4分)
∴PF=2∴△PEF的边长为2. (4分) ∴
∴

 ,∴
,∴
 ,即
,即
 ,∴
,∴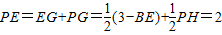 ,∴PH-BE=1
,∴PH-BE=1 ,∴
,∴ ,
, ,∵△PEF是等边三角形,∴∠4=∠5=60°
,∵△PEF是等边三角形,∴∠4=∠5=60° ,∴
,∴
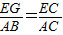 ,即
,即 ,∴
,∴
 ,∴PH-BE=1 (14分)
,∴PH-BE=1 (14分)

科目:初中数学 来源: 题型:
 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
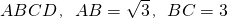 ,在BC上取两点E,F(E在F左边),
,在BC上取两点E,F(E在F左边), 以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.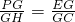 ;
;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.
的一动点(不含端点B、C),以AE为边在直线l的上方作矩形AEFG,使顶点G恰好落在射线CD上.查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市十五中中考数学模拟试卷(3月份)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年广东省广州市越秀区中考数学一模试卷(解析版) 题型:解答题
 ,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com