
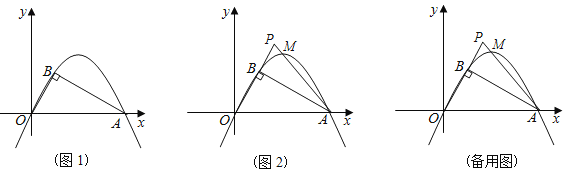
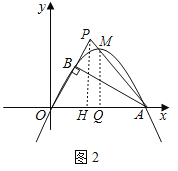
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2+bxОЙ§дЕуOКЭЕуAЃЈ12ЃЌ0ЃЉЃЌдкBдкХзЮяЯпЩЯЃЌвбжЊOBЁЭBAЃЌЧвЁЯAЃН30ЁуЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЮЊOBбгГЄЯпЩЯвЛЕуЃЌШєСЌНгAPНЛХзЮяЯпгкЕуMЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЕуMЕФКсзјБъЮЊmЃЌЪдгУКЌгаtЕФДњЪ§ЪНБэЪОmЃЌВЛвЊЧѓаДШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЙ§ЕуOзїOWЁЭAPгкWЃЌВЂНЛЯпЖЮABгкЕуGЃЌЙ§ЕуWЕФжБЯпНЛOPбгГЄЯпгкЕуNЃЌНЛxжсгкЕуKЃЌШєЁЯWKAЃН2ЁЯOAPЃЌЧвNKЃН11ЃЌЧѓЕуMЕФКсзјБъМАWGЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() ЃЛЃЈ2ЃЉmЃН
ЃЛЃЈ2ЃЉmЃН![]() ЃЛЃЈ3ЃЉMЕуЕФКсзјБъЮЊ
ЃЛЃЈ3ЃЉMЕуЕФКсзјБъЮЊ![]() ЃЌWGЃН
ЃЌWGЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіЕуBЕФзјБъЃЌНЋAЃЌBСНЕуЕФзјБъДњШыХзЮяЯпyЃНax2+bxМДПЩЕУНтЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPHЁЭOAгкЕуHЃЌЙ§ЕуMзїMQЁЭOAгкЕуQЃЌP(tЃЌ![]() t)ЃЌM(mЃЌЉ
t)ЃЌM(mЃЌЉ![]() )ЃЌгЩPHЁЮMQПЩЕУ
)ЃЌгЩPHЁЮMQПЩЕУ![]() ЃЌдђПЩЕУГіД№АИЃЛ
ЃЌдђПЩЕУГіД№АИЃЛ
ЃЈ3ЃЉШЁOAЕФжаЕуRЃЌСЌНсWRЃЌжЄЕУWRЃНWKЃЌЧѓГіWNЃН11Љ6ЃН5ЃЌПЩжЄУїЁЯPOWЃН2ЁЯNЃЌШЁOPЕФжаЕуЃЌСЌНсTWЃЌжЄЕУЁЯNЃНЁЯNTWЃЌЧѓГіOPЃН10ЃЌПЩЧѓГіtЃЌmЕФжЕЃЌЧѓГіtan![]() ЃЌдђOWЃН12ЁС
ЃЌдђOWЃН12ЁС![]() ЃЌПЩЧѓГіOGЕФГЄЃЌдђД№АИПЩЧѓГіЃЎ
ЃЌПЩЧѓГіOGЕФГЄЃЌдђД№АИПЩЧѓГіЃЎ
НтЃКЃЈ1ЃЉЙ§ЕуBзїBDЁЭOAгкЕуDЃЌ
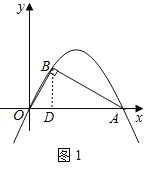
ЁпA(12ЃЌ0)ЃЌ
ЁрOAЃН12ЃЌ
ЁпЁЯAЃН30ЁуЃЌ
ЁрOB=6ЃЌ
ЁрAB=6![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрB(3ЃЌ3![]() )ЃЌ
)ЃЌ
ЁпХзЮяЯпyЃНax2+bxОЙ§ЕуB(3ЃЌ3![]() )КЭЕуA(12ЃЌ0)ЃЌ
)КЭЕуA(12ЃЌ0)ЃЌ
Ёр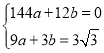 ЃЌ
ЃЌ
НтЕУ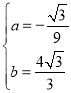 ЃЌ
ЃЌ
ЁрyЃНЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPHЁЭOAгкЕуHЃЌЙ§ЕуMзїMQЁЭOAгкЕуQЃЌP(tЃЌ![]() t)ЃЌM(mЃЌЉ
t)ЃЌM(mЃЌЉ![]() )ЃЌ
)ЃЌ
ЁпPH//MQЃЌ
ЁрЁЯAPH=ЁЯAMQЃЌ
ЁпЁЯAHP=ЁЯAQM=90ЁуЃЌ
ЁрЁїAPHЁзЁїAMQЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр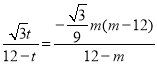 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДmЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШЁOAЕФжаЕуRЃЌСЌНсWRЃЌ
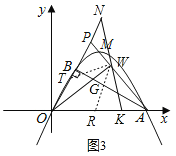
ЁпOWЁЭAPЃЌ
ЁрWRЃНRAЃНORЃЌ
ЁрЁЯOAPЃНЁЯRWAЃЌ
ЁрЁЯORWЃН2ЁЯOAPЃЌ
ЁпЁЯWKAЃН2ЁЯOAPЃЌ
ЁрЁЯORWЃНЁЯWKAЃЌ
ЁрЁЯWRKЃНЁЯWKOЃЌ
ЁрWRЃНWKЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрNWЃНNKЉWKЃН11Љ6ЃН5ЃЌ
ЁпЁЯPOWЃНЁЯBAWЃНЁЯOAPЉЁЯOABЃНІСЉ30ЁуЃЌ
ЁЯNЃНЁЯAKWЉЁЯAOBЃН2ІСЉ60ЁуЃЌ
ЁрЁЯPOWЃН2ЁЯNЃЌ
ШЁOPЕФжаЕуЃЌСЌНсTWЃЌ
ЁрЁЯNЃНЁЯNTWЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрOPЃН10ЃЌ
Ёрt2+3t2ЃН100ЃЌ
ЁрtЃН5ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЎ
ЃЎ
МДMЕуЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
ЁрЕуPЕНxжсЕФОрРыЪЧ5![]() ЃЌ
ЃЌ
Ёрtan![]() ЃЌ
ЃЌ
ЁрOWЃКAWЃКOAЃН5![]() ЃК7ЃК2
ЃК7ЃК2![]() ЃЌ
ЃЌ
ЁрOWЃН12ЁС![]() ЃЌ
ЃЌ
гжЁп![]() ЃЌ
ЃЌ![]() ЃЌOAЃН12ЃЌ
ЃЌOAЃН12ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрWGЃН![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНУћЭЌбЇЗжБ№Нјаа6ДЮЩфЛїбЕСЗЃЌбЕСЗГЩМЈЃЈЕЅЮЛЃКЛЗЃЉШчЯТБэ
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | ЕкЫФДЮ | ЕкЮхДЮ | ЕкСљНЛ | |
Мз | 9 | 8 | 6 | 7 | 8 | 10 |
вв | 8 | 7 | 9 | 7 | 8 | 8 |
ЖдЫћУЧЕФбЕСЗГЩМЈзїШчЯТЗжЮіЃЌЦфжаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ЫћУЧбЕСЗГЩМЈЕФЦНОљЪ§ЯрЭЌ B. ЫћУЧбЕСЗГЩМЈЕФжаЮЛЪ§ВЛЭЌ
C. ЫћУЧбЕСЗГЩМЈЕФжкЪ§ВЛЭЌ D. ЫћУЧбЕСЗГЩМЈЕФЗНВюВЛЭЌ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППРяЪаФГЮФОпЕъФГжжаЭКХЕФМЦЫуЦїУПжЛНјМл12дЊЃЌЪлМл20дЊЃЌЖрТђгХЛнЃЌгХЪЦЗНЗЈЪЧЃКЗВЪЧвЛДЮТђ10жЛвдЩЯЕФЃЌУПЖрТђвЛжЛЃЌЫљТђЕФШЋВПМЦЫуЦїУПжЛОЭНЕМл0.1дЊЃЌР§ШчЃКФГШЫТђ18жЛМЦЫуЦїЃЌгкЪЧУПжЛНЕМл0.1ЁСЃЈ18Љ10ЃЉ=0.8ЃЈдЊЃЉЃЌвђДЫЫљТђЕФ18жЛМЦЫуЦїЖМАДУПжЛ19.2дЊЕФМлИёЙКТђЃЌЕЋЪЧУПжЛМЦЫуЦїЕФзюЕЭЪлМлЮЊ16дЊЃЎ
ЃЈ1ЃЉЧѓвЛДЮжСЩйЙКТђЖрЩйжЛМЦЫуЦїЃЌВХФмвдзюЕЭМлЙКТђЃП
ЃЈ2ЃЉЧѓаДГіИУЮФОпЕъвЛДЮЯњЪлxЃЈxЃО10ЃЉжЛЪБЃЌЫљЛёРћШѓyЃЈдЊЃЉгыxЃЈжЛЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉвЛЬьЃЌМзЙЫПЭЙКТђСЫ46жЛЃЌввЙЫПЭЙКТђСЫ50жЛЃЌЕъжїЗЂЯжТє46жЛзЌЕФЧЎЗДЖјБШТє50жЛзЌЕФЧЎЖрЃЌЧыФуЫЕУїЗЂЩњетвЛЯжЯѓЕФдвђЃЛЕБ10ЃМxЁм50ЪБЃЌЮЊСЫЛёЕУзюДѓРћШѓЃЌЕъМввЛДЮгІТєЖрЩйжЛЃПетЪБЕФЪлМлЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦѓвЕЩшМЦСЫвЛПюЙЄвеЦЗЃЌУПМўЕФГЩБОЪЧ50дЊЃЌЮЊСЫКЯРэЖЈМлЃЌЭЖЗХЪаГЁНјааЪдЯњЃЎОнЪаГЁЕїВщЃЌЯњЪлЕЅМлЪЧ100дЊЪБЃЌУПЬьЕФЯњЪлСПЪЧ50МўЃЌЖјЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌУПЬьОЭПЩЖрЪлГі5МўЃЌЕЋвЊЧѓЯњЪлЕЅМлВЛЕУЕЭгкГЩБОЃЎ
![]() ЧѓГіУПЬьЕФЯњЪлРћШѓ
ЧѓГіУПЬьЕФЯњЪлРћШѓ![]() дЊ
дЊ![]() гыЯњЪлЕЅМл
гыЯњЪлЕЅМл![]() дЊ
дЊ![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
![]() ЧѓГіЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЧѓГіЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
![]() ШчЙћИУЦѓвЕвЊЪЙУПЬьЕФЯњЪлРћШѓВЛЕЭгк4000дЊЃЌЧвУПЬьЕФзмГЩБОВЛГЌЙ§7000дЊЃЌФЧУДЯњЪлЕЅМлгІПижЦдкЪВУДЗЖЮЇФкЃП
ШчЙћИУЦѓвЕвЊЪЙУПЬьЕФЯњЪлРћШѓВЛЕЭгк4000дЊЃЌЧвУПЬьЕФзмГЩБОВЛГЌЙ§7000дЊЃЌФЧУДЯњЪлЕЅМлгІПижЦдкЪВУДЗЖЮЇФкЃП![]() УПЬьЕФзмГЩБО
УПЬьЕФзмГЩБО![]() УПМўЕФГЩБО
УПМўЕФГЩБО![]() УПЬьЕФЯњЪлСП
УПЬьЕФЯњЪлСП![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
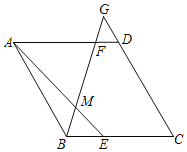
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌEдкBCЩЯЃЌGдкCDбгГЄЯпЩЯЃЌAEКЭBGЯрНЛгкЕуMЃЌШєAEЃНBGЃЌtanЁЯBMEЃН2ЃЌСтаЮABCDУцЛ§ЮЊ![]() ЃЌдђABЕФГЄ_____ЃЎ
ЃЌдђABЕФГЄ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧаЁУїЩшМЦЕФЁАЙ§жБЯпЭтвЛЕузївбжЊжБЯпЕФЦНааЯпЁБЕФГпЙцзїЭМЙ§ГЬ.
вбжЊЃКжБЯп![]() МАжБЯп
МАжБЯп![]() ЭтвЛЕуP.
ЭтвЛЕуP.

ЧѓзїЃКжБЯп![]() ЃЌЪЙ
ЃЌЪЙ![]() .
.
зїЗЈЃКШчЭМЃЌ

ЂйдкжБЯп![]() ЩЯШЁвЛЕуOЃЌвдЕуOЮЊдВаФЃЌ
ЩЯШЁвЛЕуOЃЌвдЕуOЮЊдВаФЃЌ![]() ГЄЮЊАыОЖЛАыдВЃЌНЛжБЯп
ГЄЮЊАыОЖЛАыдВЃЌНЛжБЯп![]() гк
гк![]() СНЕуЃЛ
СНЕуЃЛ
ЂкСЌНг![]() ЃЌвдBЮЊдВаФЃЌ
ЃЌвдBЮЊдВаФЃЌ![]() ГЄЮЊАыОЖЛЛЁЃЌНЛАыдВгкЕуQЃЛ
ГЄЮЊАыОЖЛЛЁЃЌНЛАыдВгкЕуQЃЛ
ЂлзїжБЯп![]() .
.
ЫљвджБЯп![]() ОЭЪЧЫљЧѓзїЕФжБЯп.
ОЭЪЧЫљЧѓзїЕФжБЯп.
ИљОнаЁУїЩшМЦЕФГпЙцзїЭМЙ§ГЬЃК
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУї
жЄУїЃКСЌНг![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() __________.
__________.
Ёр![]() ЃЈ______________ЃЉЃЈЬюЭЦРэЕФвРОнЃЉ.
ЃЈ______________ЃЉЃЈЬюЭЦРэЕФвРОнЃЉ.
Ёр![]() ЃЈ_____________ЃЉЃЈЬюЭЦРэЕФвРОнЃЉ.
ЃЈ_____________ЃЉЃЈЬюЭЦРэЕФвРОнЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЕФЕуPКЭЭМаЮMЃЌИјГіШчЯТЕФЖЈвхЃКШєдкЭМаЮMДцдквЛЕуQЃЌЪЙЕУPЁЂQСНЕуМфЕФОрРыаЁгкЛђЕШгк1ЃЌдђГЦPЮЊЭМаЮMЕФЙиСЊЕуЃЎ
жаЕФЕуPКЭЭМаЮMЃЌИјГіШчЯТЕФЖЈвхЃКШєдкЭМаЮMДцдквЛЕуQЃЌЪЙЕУPЁЂQСНЕуМфЕФОрРыаЁгкЛђЕШгк1ЃЌдђГЦPЮЊЭМаЮMЕФЙиСЊЕуЃЎ
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ2ЪБЃЌ
ЂйдкЕу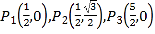 жаЃЌЁбOЕФЙиСЊЕуЪЧ_______________ЃЎ
жаЃЌЁбOЕФЙиСЊЕуЪЧ_______________ЃЎ
ЂкЕуPдкжБЯпy=-xЩЯЃЌШєPЮЊЁбO ЕФЙиСЊЕуЃЌЧѓЕуPЕФКсзјБъЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЁбC ЕФдВаФдкxжсЩЯЃЌАыОЖЮЊ2ЃЌжБЯпy=-x+1гыxжсЁЂyжсНЛгкЕуAЁЂBЃЎШєЯпЖЮABЩЯЕФЫљгаЕуЖМЪЧЁбCЕФЙиСЊЕуЃЌжБНгаДГідВаФCЕФКсзјБъЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2+bx+cШчЭМЃЌдђДњЪ§ЪНЂйacЃЛЂкa+b+cЃЛЂл4aЉ2b+cЃЛЂм2a+bЦфжЕДѓгк0ЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
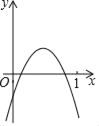
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
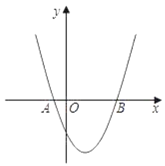
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНx2+bx+cОЙ§A(Љ1ЃЌ0)ЁЂB(3ЃЌ0)СНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖЅЕузјБъЃЛ
ЃЈ2ЃЉШєpЮЊxжсЩЯЗНХзЮяЯпЩЯвЛЕуЃЌЧвШ§НЧаЮPABУцЛ§ЮЊ20ЃЌЧѓPЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com