
【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )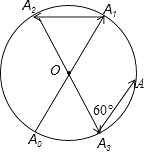
A.4
B.2 ![]()
C.2
D.0
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=α,E为对角线AC上的一点(不与A,C重合),将射线EB绕点E顺时针旋转β角之后,所得射线与直线AD交于F点.试探究线段EB与EF的数量关系.小宇发现点E的位置,α和β的大小都不确定,于是他从特殊情况开始进行探究.
(1)如图1,当α=β=90°时,菱形ABCD是正方形.小宇发现,在正方形中,AC平分∠BAD,作EM⊥AD于M,EN⊥AB于N.由角平分线的性质可知EM=EN,进而可得△EMF≌△ENB,并由全等三角形的性质得到EB与EF的数量关系为 .
(2)如图2,当α=60°,β=120°时,
①依题意补全图形;
②请帮小宇继续探究(1)的结论是否成立.若成立,请给出证明;若不成立,
请举出反例说明;
(3)小宇在利用特殊图形得到了一些结论之后,在此基础上对一般的图形进行了探究,设∠ABE=γ,若旋转后所得的线段EF与EB的数量关系满足(1)中的结论,请直接写出角α,β,γ满足的关系:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式x2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
x2+bx+c | … | 3 | ﹣1 | 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y>0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中: ①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 . (请写出所有正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过点A(﹣2,0)的直线交y轴正半轴于点B,将直线AB绕着点顺时针旋转90°后,分别与x轴、y轴交于点D、C.
(1)若OB=4,求直线AB的函数关系式;
(2)连接BD,若△ABD的面积是5,求点B的运动路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( ) 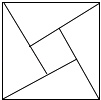
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC、AC分别交于D、E两点,过点D作DF⊥AC,垂足为点F. 
(1)求证:DF是⊙O的切线;
(2)若AE=4,cosA= ![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与x之间的函数图象是( )
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com