
 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.| BC |
| BC+OB |
| AB |
| OS |
| 1 |
| 1+OB |
| 1.5 |
| h |
| 2 |
| 3 |
| B′C′ |
| B′C′+BB′+OB |
| A′B′ |
| OS |
| 1.8 |
| 1.8+4+OB |
| 1.5 |
| h |
| 1.8 | ||
5.8+
|
| 1.5 |
| h |


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源:2012-2013学年江苏兴化市安丰中学八年级下学期第二次月考数学试卷(带解析) 题型:解答题
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB‘),再把竹竿竖立在地面上,测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省泰州市姜堰区四校八年级下学期第三次联考数学试卷(带解析) 题型:解答题
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB‘),再把竹竿竖立在地面上, 测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.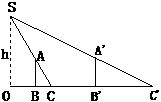
查看答案和解析>>
科目:初中数学 来源:2014届江苏兴化市八年级下学期第二次月考数学试卷(解析版) 题型:解答题
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB‘),再把竹竿竖立在地面上,测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.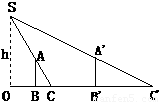
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
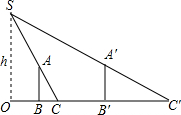 为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.
为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com