

分析 (1)先根据旋转30°,求得∠COP的度数,再判定△BOC是等边三角形,求得∠OCB的度数,最后根据三角形外角性质,求得∠P的度数;
(2)先根据等腰三角形BOC,利用三线合一,求得∠COD的度数为$\frac{1}{2}$(90°-α),再根据OP平分∠AOC,求得∠POC=$\frac{1}{2}$α,最后根据∠POD=∠POC+∠COD,求得∠POD为45°,进而根据∠P与∠POD互余,求得∠P的度数;
(3)选择A题,先判定△AOP≌△COP(SAS),得出∠APB=90°,再根据勾股定理得到:PA2+PB2=AB2=OA2+OB2,根据OA=OB=1,进行计算即可.选择B题,先判定△ODP为等腰直角三角形,求得∠P的度数,再根据PC2+PB2=(PD+BD)2+(PD-BD)2进行推导即可得出结论.
解答 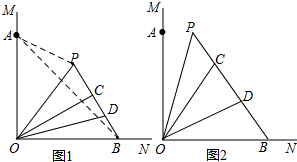 解:(1)如图2,若α=30°,则∠COP=$\frac{1}{2}$∠AOC=15°,∠BOC=60°,
解:(1)如图2,若α=30°,则∠COP=$\frac{1}{2}$∠AOC=15°,∠BOC=60°,
∵CO=AO=BO,
∴△BOC是等边三角形,
∴∠OCB=60°,
∴∠P的度数为:60°-15°=45°,
故答案为:45°;
(2)证明:由旋转得,OA=OC,∠AOC=α,
∵OA=OB,
∴OC=OB,
∵点D是线段BC的中点,
∴OD⊥BC,∠COD=∠BOD=$\frac{1}{2}$∠BOC,
∵∠AOB=90°,
∴∠COD=$\frac{1}{2}$(90°-α),
∵OP平分∠AOC,
∴∠POC=$\frac{1}{2}$α,
∴∠POD=∠POC+∠COD=45°,
∵∠ODP=90°,
∴∠P=90°-45°=45°;
(3)选择A题.
如图1,连接AB、AP,
∵OP平分∠AOC,
∴∠AOP=∠COP,
在△AOP和△COP中,
$\left\{\begin{array}{l}{OA=OC}\\{∠AOP=∠COP}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△COP(SAS),
∴∠APO=∠CPO=45°,
∴∠APB=90°,
∴在Rt△APB中,由勾股定理得,PA2+PB2=AB2,
∵在Rt△AOB中,由勾股定理得,AB2=OA2+OB2=12+12=2,
∴PA2+PB2=2.
选择B题.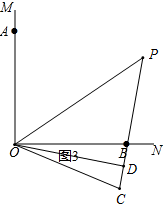
①∠P=45°.
理由:如图3,根据旋转可得,OC=OA=OB,
∵D是BC中点,
∴OD⊥BC,即∠ODP=90°,
且OD平分∠BOC,
又∵OP平分∠AOC,
∴∠DOP=∠COP-∠COD=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°,
∴Rt△ODP中,∠P=45°;
②PC2+PB2的值为2.
理由:∵OD⊥BC,∠P=45°,
∴△OPD是等腰直角三角形,
∴PD=OD,
∵PC=PD+BD,PB=PD-BD,
∴PC2+PB2
=(PD+BD)2+(PD-BD)2
=2PD2+2BD2
=2(PD2+BD2)
=2(OD2+BD2)
=2×OB2
=2×12
=2
故PC2+PB2的值为2.
点评 本题以旋转为背景,主要考查了等边三角形、全等三角形以及勾股定理的综合应用.在图形的旋转过程中,旋转前、后的图形全等,故对应角相等,对应边相等,这是解决旋转问题的关键.等边三角形的角的特殊性给有关角的计算奠定了基础,它的边角性质为证明线段、角相等提供了便利条件,等边三角形具备三线合一的性质,解题时要善于挖掘图形中的隐含条件.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:选择题
 如图,郑梦将一个三角形纸板ABC沿直线BC向右平移得到新的三角形DEF,使点E与点C重合,经测量得到∠BAC=40°,EF=4cm,三角形ABC的周长为16cm,连接AD,则下列说法中不正确的是( )
如图,郑梦将一个三角形纸板ABC沿直线BC向右平移得到新的三角形DEF,使点E与点C重合,经测量得到∠BAC=40°,EF=4cm,三角形ABC的周长为16cm,连接AD,则下列说法中不正确的是( )| A. | ∠EDF=45° | B. | AB∥CD | ||
| C. | 四边形ABFD的周长为20cm | D. | AD∥BF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,四边形ABCD中,AB∥OC,BC∥AO,A、C两点的坐标分别为(-$\sqrt{3}$,$\sqrt{5}$)、(-2$\sqrt{3}$,0),A、B两点间的距离等于O、C两点间的距离.
如图所示,四边形ABCD中,AB∥OC,BC∥AO,A、C两点的坐标分别为(-$\sqrt{3}$,$\sqrt{5}$)、(-2$\sqrt{3}$,0),A、B两点间的距离等于O、C两点间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 贵阳市某中学初一年级的学生参加军训,在一次野外生存训练中,教官将一包食品随意埋在如图所示的区域中(图中每个三角形的大小、形状完全相同).
贵阳市某中学初一年级的学生参加军训,在一次野外生存训练中,教官将一包食品随意埋在如图所示的区域中(图中每个三角形的大小、形状完全相同).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
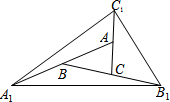 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )| A. | 7 | B. | 14 | C. | 49 | D. | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰Rt△OAB中,∠OAB=90°,顶点A在y=-$\frac{12}{x}$(x<0)上,顶点B在y=$\frac{k}{x}$(x>0)上,若△OAB的面积是$\frac{25}{2}$,则k的值是7.
如图,等腰Rt△OAB中,∠OAB=90°,顶点A在y=-$\frac{12}{x}$(x<0)上,顶点B在y=$\frac{k}{x}$(x>0)上,若△OAB的面积是$\frac{25}{2}$,则k的值是7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com