
如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.

(1)求证:AD∥OC;
(2)若AE=2 ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
 每课必练系列答案
每课必练系列答案科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:解答题
如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD、小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1: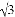 ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: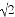 ≈1.414,
≈1.414,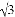 ≈1.732.)
≈1.732.)

查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
用A,B,C分别表示学校、小明家、小红家,已知学校在小明家的南偏东25°,小红家在小明家的北偏东35°,则∠ABC等于( )
A. 35° B. 120° C. 105° D. 115°
B 【解析】试题分析:根据题意可得:∠DBC=35°,∠ABE=25°,根据∠ABC=180°-∠DBC-∠ABE得出答案,故选择B.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:单选题
已知关于x的分式方程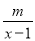 +
+ =1的解是非负数,则m的取值范围是( )
=1的解是非负数,则m的取值范围是( )
A. m>2 B. m≥2 C. m≥2且m≠3 D. m>2且m≠3
C 【解析】试题解析:分式方程去分母得:m-3=x-1, 解得:x=m-2, 由方程的解为非负数,得到m-2≥0,且m-2≠1, 解得:m≥2且m≠3. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:单选题
下列运算结果正确的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=3.
(1)以BC边上一点O为圆心作⊙O,使⊙O分别与AC、AB都相切 (要求:尺规作图,保留作图痕迹,不写作法) ;
(2)求⊙O的面积.

查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:填空题
若一元二次方程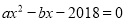 有一根为
有一根为 ,则
,则 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:解答题
如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.

查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:解答题
计算:|﹣2|+ ﹣(﹣1)2017.
﹣(﹣1)2017.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com