
����Ŀ����֪�����Ķ�������n���ε����ĵ�O�����������Ŷ���O��ת���ǵ���������n�� �ε����߷ֱ��ڵ�M��N����������n�����ص��������ΪS��
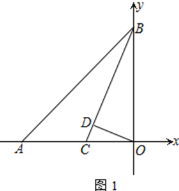
��1����n=4���߳�Ϊ2������=90��ʱ����ͼ��1������ֱ��д��S��ֵ��

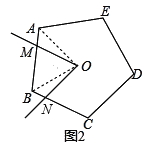
��2����n=5������=72��ʱ����ͼ��2������������ת�����У�S�Ƿ����仯����˵�����ɣ�

��3����n=6������=120��ʱ����ͼ��3���������S��ԭ������������ļ���֮��������˵�����ɣ�����������ƽ������BC�߽��ڵ�P���ж��ı���OMPN����״����˵�����ɣ�

���𰸡���1��1����2�����䣻��3��![]() ���ı���OMPN�����Σ�
���ı���OMPN�����Σ�
��������
��1����ͼ1�����ӶԽ���OA��OB��֤����AOM����BON��ASA������S��AOM=S��BON�� ����S=S��ABO= ![]() S������ABCD=
S������ABCD= ![]() ��4=1��
��4=1��
��2����ͼ2������ת�����У���������n�����ص����ֵ����S���䣬����OA��OB��ͬ��֤����OAM����OBN����S=S��OBN+S��OBM=S��OAM+S��OBM=S��OAB����S�Ĵ�С���䣻
��3����ͼ3��120���൱���������Ľǣ���������Ϊһ�����Ľ�������ת���Σ���ǰ���ʵ������ã���תһ�����Ľ�ʱ�ص����ֵ������ԭ����n��������� ![]() ����S��ԭ�������������
����S��ԭ�������������![]() ��Ҳ������ȣ�1����2��֤����OAM����OBN�����ø��������ۣ�
��Ҳ������ȣ�1����2��֤����OAM����OBN�����ø��������ۣ�
�ı���OMPN�����Σ�
�������£���ͼ4����������ƽ������BC�߽��ڵ�P���������߹���ȫ�������Σ�ͬ��֤����OAM����OBP����OCN������OMP����OPN���ǵȱ������Σ���OM=PM=OP=ON=PN�������ı���ȵ��ı������οɵã��ı���OMPN�����Σ�
��1���⣺��ͼ1������OA��OB��
��n=4ʱ���ı���ABCD�������Σ�
��OA=OB��AO��BO��
���AOB=90�㣬
���AON+��BON=90�㣬
�ߡ�MON=����=90�㣬
���AON+��AOM=90�㣬
���BON=��AOM��
��O��������ABCD�����ģ�
���OAM=��ABO=45�㣬
�ڡ�AOM�͡�BON�У�
�� 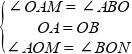 ��
��
���AOM�ա�BON��ASA����
��S��AOM=S��BON��
��S��AOM+S��AON=S��BON+S��AON��
��S�ı���ANDM=S��ABO=S��
��������ABCD�ı߳�Ϊ2��
��S������ABCD=2��2=4��
��S=S��ABO= ![]() S������ABCD=
S������ABCD= ![]() ��4=1��
��4=1��

��2���⣺��ͼ2������ת�����У���������n�����ص����ֵ����S���䣬
�������£�����OA��OB��
��OA=OB=OC����AOB=��MON=72�㣬
���AOM=��BON���ҡ�OAB=��OBC=54�㣬
���OAM�ա�OBN��
���ı���OMBN�������S=S��OBN+S��OBM=S��OAM+S��OBM=S��OAB��
��S�Ĵ�С���䣻
��3���⣺���룺S��ԭ�������������![]() �������ǣ�
�������ǣ�
��ͼ3������OB��OD��
ͬ���á�BOM�ա�DON��
��S=S��BOM+S�ı���OBCN=S��DON+S�ı���OBCN=S�ı���OBCD= ![]() S������ABCDEF��
S������ABCDEF��
�ı���OMPN�����Σ�
�������£�
��ͼ4����������ƽ������BC�߽��ڵ�P��
����OA��OB��OC��OD��PM��PN��
��OA=OB=OC=OD����AOB=��BOC=��COD=��MOP=��PON=60�㣬
���OAM=��OBP=��OCN=60�㣬��AOM=��BOP=��CON��
���OAM�ա�OBP�ա�OCN��
��OM=OP=ON��
���OMP�͡�OPN���ǵȱ������Σ�
��OM=PM=OP=ON=PN��
���ı���OMPN�����Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˳��ijУ��֪��ѧ������ңԶ�ĺ�ͼ�������������۹������ȼ�������Ʒ�Ƶ��˽�̶ȣ������ȡ�˲���ѧ�������ʾ����飬�ʾ����ĸ�ѡ�ÿλ�������ѧ����ѡ��ֻѡһ�A��ʮ���˽⣬B���˽�϶࣬C���˽���٣�D����֪����������Ľ�����Ƴ�����������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
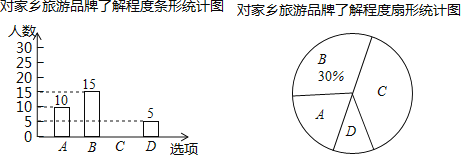
��1�����ε����˶�����ѧ����
��2����ȫ����ͳ��ͼ��
��3����У����500��ѧ�������������ʮ���˽�����ѧ���ж�������
��4���ڱ�������ʮ���˽�����ѧ����������ѧ����ɲ�����������3��������1��Ů����ѧУ�����4������ѡ��������������Ʒ������Ա�������б�����״ͼ�������ѡ�е�����ǡ����һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��ABC�͡�BDE���ǵȱ������Ρ������н��ۣ���AE=CD.��BF=BG.��HB��FG.�ܡ�AHC=60.�ݡ�BFG�ǵȱ������Σ�������ȷ����___.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
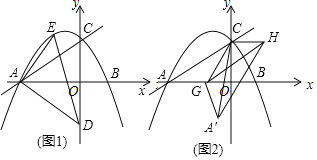
����Ŀ����ͼ��������y=��![]() x2��
x2��![]() x+
x+![]() ��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C��
��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C��
��1����������ߵĶԳ�����߶�AB�ij���
��2����ͼ1����֪��D��0����![]() ������E��ֱ��AC�Ϸ��������ϵ�һ���㣬����AED����������ֵ��
������E��ֱ��AC�Ϸ��������ϵ�һ���㣬����AED����������ֵ��
��3����ͼ2����G���߶�AB�ϵ�һ���㣬��H�ڵ�һ���ޣ�AC��GH��AC=GH����ACG����A��CG����ֱ��CG�Գƣ��Ƿ���ڵ�G��ʹ����A��CH��ֱ�������Σ������ڣ���ֱ��д����G�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʡij���ճ�Ϊȫ�˻������һ��ɱ�Ϊÿ��20Ԫ�ù���Ʒ��Ͷ���г�������������ÿ���������y���������ۼ�x��Ԫ�M������һ�κ��������ۼ�Ϊ22Ԫ�M��ʱ��ÿ��������Ϊ780�������ۼ�Ϊ25Ԫ�M��ʱ��ÿ���������Ϊ750����
��1����y��x�ĺ�����ϵʽ��
��2������ù���Ʒ�ۼ���߲��ܳ���ÿ��30Ԫ����ô�ۼ۶�Ϊÿ������Ԫʱ�����ճ����۸ù���Ʒÿ���õ����������������Ƕ���Ԫ��������=�ۼ۩��ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A(��t��0)��B(0��t)������t��0����CΪOA��һ�㣬OD��BC�ڵ�D���ҡ�BCO=45������COD
(1) ��֤��BCƽ�֡�ABO
(2) ��![]() ��ֵ
��ֵ
(3) ����PΪ����������һ���㣬�ҡ�APO=135��������AP��BP�Ƿ����ij��ȷ����λ�ù�ϵ��˵������
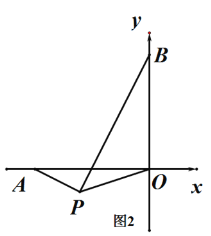
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC �ֱ��� AB��AC ���۵õ���ABD ����AEC���߶� BD ��AE ���ڵ� F��
��1������ABC=16����ACB=30�������DAE ����BFE ��ֵ��
��2���� BD �� CE ���ڵ�ֱ���ഹֱ�����CAB �Ķ�����
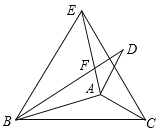
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����D��E��F�ֱ���AB��BC��AC���ϣ���BE=CF��BD=CE.
��1����֤����DEF�ǵ��������Σ�
��2������A=50��ʱ�����DEF�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��һ�κ���y=kx+b��k��bΪ������k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=![]() ��nΪ������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ��ֱΪD����OB=2OA=3OD=6��
��nΪ������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ��ֱΪD����OB=2OA=3OD=6��
��1����һ�κ����뷴���������Ľ���ʽ��
��2����������ͼ�����һ���������ꣻ
��3��ֱ��д������ʽ��kx+b��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com