
【题目】在△ABC中,∠C=90°,∠BAC=60°,△ABC绕点C顺时针旋转,旋转角为α(0°<α<180°),点A、B的对应点分别是点D、E.
(1)如图1,当点D恰好落在边AB上时,试判断DE与AC的位置关系,并说明理由.
(2)如图2,当点B、D、E三点恰好在一直线上时,旋转角α=__°,此时直线CE与AB的位置关系是__.
(3)在(2)的条件下,联结AE,设△BDC的面积S1,△AEC的面积S2,则S1与S2的数量关系是_____.
(4)如图3,当点B、D、E三点不在一直线上时,(3)中的S1与S2的数量关系仍然成立吗?试说明理由.

【答案】 (1)DE∥AC (2) 120° EC⊥AB. S1=S2) (4) S1=S2仍然成立
【解析】试题分析:
(1)由旋转的性质可得∠EDC=∠BAC,DC=AC结合∠BAC=60°,可得△ADC是等边三角形,从而可得∠DCA=∠EDC=60°,由此可得DE∥AC;
(2)如下图2,在△ABC中,由∠C=90°,∠BAC=60°可得∠ABC=30°,延长EC交AB于点F,由旋转的性质可得CE=BE,∠E=∠ABC=30°,结合B、D、E的三点在同一直线上可得∠CBE=∠E=30°,从而可得旋转角∠BCE=120°,结合∠BCE=∠ABC+∠BFC,∠ABC=30°,可得∠BFC=90°,从而可得EC⊥AB;
(3)如上图2,过点D作DH⊥BC于点H,由∠DCF=∠ACB=90°易得∠ACF=∠DCH,结合∠AFC=∠DHC=90°,AC=DC可得△ACF≌△DCH,从而可得AF=DH,结合BC=EC即可得到S1=S2;
(4)如下图3,过D作DH⊥BC于H,过A作AG⊥EC交EC的延长线于G,与(3)同理可得△AGC≌△DHC,从而可得AG=HD,结合EC=BC即可得到S1=S2仍然成立.
试题解析:
(1)DE∥AC.理由:∵△ABC旋转后与△DCE全等,
∴∠A=∠CDE,AC=DC.
∵∠BAC=60°,AC=DC,
∴△DAC是等边三角形.
∴∠DCA=60°.
又∵∠CDE=∠BAC=60°,
∴∠DCA=∠CDE=60°,
∴DE∥AC.
(2)120°;EC⊥AB,理由如下:
如下图2,延长EC交AB于点F,
∵在△ABC中,由∠C=90°,∠BAC=60°,
∴∠ABC=30°,
由旋转的性质可得:CE=BE,∠E=∠ABC=30°,
∵B、D、E的三点在同一直线上,
∴∠CBE=∠E=30°,
∴旋转角∠BCE=120°,
又∵∠BCE=∠ABC+∠BFC,∠ABC=30°,
∴∠BFC=120°-30°=90°,
∴EC⊥AB于点F;

(3)S1=S2,理由如下:
如上图2,连接AE,过点D作DH⊥BC于点H,
∴∠AFC=∠DHC=90°,
∵∠ACB=∠DCE=90°,
∴∠ACF=∠DCH,
又∵AC=DC,
∴△ACF≌△DCH,
∴AF=DH,
又∵EC=BC,
∴![]() CE·AF=
CE·AF=![]() BC·DH,即S1=S2;
BC·DH,即S1=S2;
(4)S1=S2仍然成立,理由如下:
如下图3所示:过D作DH⊥BC于H,过A作AG⊥EC交EC的延长线于G.
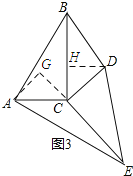
∵DH⊥BC,AG⊥EC,
∴∠AGC=∠DHC=90°
∵△ABC旋转后与△DCE全等
∴∠ACB=∠DCE=90°,AC=DC,BC=CE.
∵∠ACE+∠BCD=180°,∠GCA+∠ECA=180°,
∴∠ACG=∠DCH,
又∵∠AGC=∠DHC,AC=DC,
∴△AGC≌△DHC,
∴AG=DH,
∴![]() ECAF=
ECAF=![]() CBDG,即S1=S2.
CBDG,即S1=S2.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点 A 表示的数为 6,B 是数轴上在 A 左侧的一点,且 A, B 两点间的距离为 10.动点 P 从点 A 出发,以每秒 6 个单位长度的速度沿数轴 向左匀速运动,设运动时间为 t(t>0)秒.
(1)数轴上点 B 表示的数是 ,点 P 表示的数是 (用含 t 的代数 式表示);
(2)动点 Q 从点 B 出发,以每秒 4 个单位长度的速度沿数轴向左匀速运动,若 点 P、Q 时出发.求:
①当点 P 运动多少秒时,点 P 与点 Q 相遇?
②当点 P 运动多少秒时,点 P 与点 Q 间的距离为 8 个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB∥CD,∠A=∠C;③AO=CO,BO=DO;④AB∥CD,AD=BC.
一定能判定四边形ABCD是平行四边形的条件有----------------------------( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOB是一条直线,OC是∠AOD的平分线,OE 是∠BOD的平分线.

(1)若∠AOE=140°,求∠AOC的度数;
(2)若∠EOD :∠COD=2 : 3,求∠COD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解学生“自主学习、合作交流”的情况,对八年级各班部分同学进行了一段时间的跟踪调査,将调查结果(A:特别好; B:较好; C:一般; D:较差)绘制成以下两幅不完整的统计图. 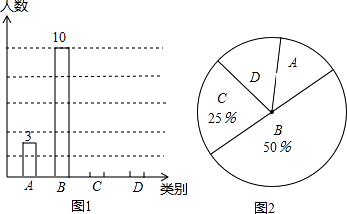
请根据图中提供的信息,解答下列问题:
(1)此次跟踪调查的学生有人;扇形统计图中,D类所占圆心角为度;
(2)补全条形统计图;
(3)如果该校八年级共有学生360人,试估计A类学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且
![]() .动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(
.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(![]() )秒.
)秒.
![]()
(1)请写出数轴上点B表示的数 ,点P表示的数 (用含t 的整式表示);
(2)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC纸片中,∠ACB=90°,AC=6,BC=8,P是AB边上一点,连接CP.沿CP把Rt△ABC纸片裁开,要使△ACP是等腰三角形,那么AP的长度是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小英在周末和爸爸妈妈以及爷爷奶奶一行6人,自驾外出旅游,出发前油箱里有油5升,在加油站加140元的油.已知油价是7元/升,目的地距离出发地320千米,正常行驶时,车子的耗油情况是0.42元/千米.
(1)在加油站加油 升;车子的耗油情况换算成 升/千米.
(2)在行驶过程中,设油箱内余油y(升),行驶路程x(千米),将y表示为x的函数.
(3)若油箱里余油量低于5升会自动报警,通过计算回答,小明他们在到达目的地之前,车子是否会自动报警.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
(1)求证:DB=DE;
(2)过点D作DF垂直BE,垂足为F,若CF=3,求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com