

 ≈1.414,
≈1.414,  ≈1.732)
≈1.732) /3=3
/3=3 =5.1(米)
=5.1(米)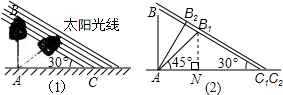
 ≈3.5(米),
≈3.5(米),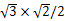 ×
×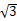 ≈6.1(米),
≈6.1(米),

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源:不详 题型:解答题
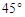 .为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为
.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为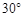 ,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?
,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1 | B.3 | C.6 | D.非以上答案 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com