
”¾ĢāÄæ”æŠĀ¶ØŅåŗÆŹż£ŗŌŚy¹ŲÓŚxµÄŗÆŹżÖŠ£¬Čō0”Üx”Ü1Ź±£¬ŗÆŹżyÓŠ×ī“óÖµŗĶ×īŠ”Öµ£¬·Ö±š¼ĒymaxŗĶymin £¬ ĒŅĀś×ć ![]() £¬ŌņĪŅĆĒ³ĘŗÆŹżyĪŖ”°Čż½ĒŠĪŗÆŹż”±£®
£¬ŌņĪŅĆĒ³ĘŗÆŹżyĪŖ”°Čż½ĒŠĪŗÆŹż”±£®
£Ø1£©ČōŗÆŹży=x+aĪŖ”°Čż½ĒŠĪŗÆŹż”±£¬ĒóaµÄȔֵ·¶Ī§£»
£Ø2£©ÅŠ¶ĻŗÆŹży=x2© ![]() x+1ŹĒ·ńĪŖ”°Čż½ĒŠĪŗÆŹż”±£¬²¢ĖµĆ÷ĄķÓÉ£»
x+1ŹĒ·ńĪŖ”°Čż½ĒŠĪŗÆŹż”±£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŅŃÖŖŗÆŹży=x2©2mx+1£¬Čō¶ŌÓŚ0”Üx”Ü1ÉĻµÄČĪŅāČżøöŹµŹża£¬b£¬cĖł¶ŌÓ¦µÄČżøöŗÆŹżÖµ¶¼Äܹ¹³ÉŅ»øöČż½ĒŠĪµÄČż±ß³¤£¬ŌņĒóĀś×ćĢõ¼žµÄmµÄȔֵ·¶Ī§£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗ”ßµ±x=0£¬ymin=a£»x=1£¬ymax=1+a£¬
”ßy=x+aĪŖČż½ĒŠĪŗÆŹż£¬
”ą ![]() £¬
£¬
”ąa£¾1£»
£Ø2£©
½ā£ŗŹĒČż½ĒŠĪŗÆŹż£¬ĄķÓÉČēĻĀ£ŗ
”߶Ō³ĘÖįĪŖÖ±Ļß ![]() £¬0”Üx”Ü1£¬
£¬0”Üx”Ü1£¬
”ąµ± ![]() £¬
£¬
”ą ![]() £¬
£¬
”ąĖüŹĒČż½ĒŠĪŗÆŹż£»
£Ø3£©
½ā£ŗ”߶ŌÓŚ0”Üx”Ü1ÉĻµÄČĪŅāČżøöŹµŹża£¬b£¬cĖł¶ŌÓ¦µÄČżøöŗÆŹżÖµ¶¼Äܹ¹³ÉŅ»øöČż½ĒŠĪµÄČż±ß³¤£¬
”ą ![]() £¬ČōaĪŖ×īŠ”£¬cĪŖ×ī“ó£¬ŌņÓŠ
£¬ČōaĪŖ×īŠ”£¬cĪŖ×ī“ó£¬ŌņÓŠ ![]() £¬Ķ¬Ąķµ±bĪŖ×īŠ”£¬cĪŖ×ī“óŹ±Ņ²æɵĆ
£¬Ķ¬Ąķµ±bĪŖ×īŠ”£¬cĪŖ×ī“óŹ±Ņ²æÉµĆ ![]() £¬
£¬
”ąy=x2©2mx+1ŹĒČż½ĒŠĪŗÆŹż£¬
”ßy=x2©2mx+1=£Øx©m£©2©m2+1£¬
”ą¶Ō³ĘÖįĪŖÖ±Ļßx=m£¬
¢Łµ±m”Ü0Ź±£¬µ±x=0£¬ymin=1£¬
µ±x=1£¬ymax=©2m+2£¬Ōņ2£¾©2m+2£¬½āµĆm£¾0£¬
”ąĪŽ½ā£»
¢Śµ± ![]() £¬
£¬ ![]() £¬µ±x=1£¬ymax=©2m+2£¬
£¬µ±x=1£¬ymax=©2m+2£¬ ![]() £¬
£¬
½āµĆ0£¼m£¼1£¬
”ą ![]() £»
£»
¢Ūµ± ![]() £¬
£¬ ![]() £¬µ±x=0£¬ymax=1£¬Ōņ
£¬µ±x=0£¬ymax=1£¬Ōņ ![]() £¬
£¬
½āµĆ ![]() £¬
£¬
”ą ![]() £»
£»
¢Üµ±m£¾1£¬µ±x=1£¬ymin=©2m+2£¬x=0£¬ymax=1£¬Ōņ ![]() £¬
£¬
½āµĆ ![]() £¬
£¬
”ąĪŽ½ā£»
×ŪÉĻŹöæÉÖŖmµÄȔֵ·¶Ī§ĪŖ ![]() »ņ
»ņ ![]() £®
£®
”¾½āĪö”æ£Ø1£©ÓÉŗÆŹżµÄŠŌÖŹæÉĒóµĆĘä×ī“óÖµŗĶ×īŠ”Öµ£¬ÓÉČż½ĒŠĪŗÆŹżµÄ¶ØŅåæɵƵ½¹ŲÓŚaµÄ²»µČŹ½×飬æÉĒóµĆaµÄȔֵ·¶Ī§£»£Ø2£©ÓÉÅ×ĪļĻß½āĪöŹ½æÉĒóµĆĘä¶Ō³ĘÖį£¬ÓÉxµÄ·¶Ī§æÉĒóµĆĘä×ī“óÖµŗĶ×īŠ”Öµ£¬Āś×ćČż½ĒŠĪŗÆŹżµÄ¶ØŅ壻£Ø3£©ÓÉČż½ĒŠĪµÄČż±ß¹ŲĻµæÉÅŠ¶ĻŗÆŹży=x2©2mx+1ĪŖČż½ĒŠĪŗÆŹż£¬ŌŁĄūÓĆČż½ĒŠĪŗÆŹżµÄ¶ØŅå·Ö±šµĆµ½¹ŲÓŚmµÄ²»µČŹ½×飬¼“æÉĒóµĆmĖłĀś×ćµÄ²»µČŹ½£¬æÉĒóµĆmµÄȔֵ·¶Ī§£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
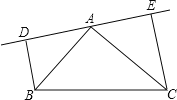
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÄŚÓŠŅ»µćD£¬ĒŅDA£½DB£½DC.Čō”ĻDAB£½20”ć£¬”ĻDAC£½30”ć£¬Ōņ”ĻBDCµÄ¶ČŹżĪŖ( )

A. 100”ć B. 80”ć C. 70”ć D. 50”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬³¤·½ŠĪÖ½Ę¬ABCDÖŠ£¬AB£½6 cm£¬BC£½8 cm£¬µćEŹĒBC±ßÉĻŅ»µć£¬Į¬½ÓAE£¬²¢½«”÷AEBŃŲAEÕŪµž£¬µĆµ½”÷AEB”䣬ŅŌC£¬E£¬B”äĪŖ¶„µćµÄČż½ĒŠĪŹĒÖ±½ĒČż½ĒŠĪŹ±£¬BEµÄ³¤ĪŖ____cm.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij»Øľ¹«Ė¾ŌŚ20ĢģÄŚĻśŹŪŅ»ÅśĀķĢćĮ«£®ĘäÖŠ£¬øĆ¹«Ė¾µÄĻŹ»ØÅś·¢²æČÕĻśŹŪĮæy1£ØĶņ¶ä£©ÓėŹ±¼äx£ØxĪŖÕūŹż£¬µ„Ī»£ŗĢģ£©²æ·Ö¶ŌÓ¦ÖµČēĻĀ±ķĖłŹ¾£®
Ź±¼äx£ØĢģ£© | 0 | 4 | 8 | 12 | 16 | 20 |
ĻśĮæy1£ØĶņ¶ä£© | 0 | 16 | 24 | 24 | 16 | 0 |
ĮķŅ»²æ·ÖĻŹ»ØŌŚĢŌ±¦ĶųĻśŹŪ£¬ĶųÉĻĻśŹŪČÕĻśŹŪĮæy2£ØĶņ¶ä£©ÓėŹ±¼äx£ØxĪŖÕūŹż£¬µ„Ī»£ŗĢģ£© ¹ŲĻµČēĶ¼ĖłŹ¾£®
£Ø1£©ĒėÄć“ÓĖłŃ§¹żµÄŅ»“ĪŗÆŹż”¢¶ž“ĪŗÆŹżŗĶ·“±ČĄżŗÆŹżÖŠČ·¶ØÄÄÖÖŗÆŹżÄܱķŹ¾y1ÓėxµÄ±ä»Æ¹ęĀÉ£¬Š“³öy1ÓėxµÄŗÆŹż¹ŲĻµŹ½¼°×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø2£©¹Ū²ģĀķĢćĮ«ĶųÉĻĻśŹŪĮæy2ÓėŹ±¼äxµÄ±ä»Æ¹ęĀÉ£¬ĒėÄćÉčĻėÉĢ¼Ņ²ÉÓĆĮĖŗĪÖÖĻśŹŪ²ßĀŌŹ¹µĆĻśŹŪĮæ·¢ÉśĮĖ±ä»Æ£¬²¢Š“³öĻśŹŪĮæy2ÓėxµÄŗÆŹż¹ŲĻµŹ½¼°×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø3£©ÉčøĆ»Øľ¹«Ė¾ČÕĻśŹŪ×ÜĮæĪŖyĶņ¶ä£¬Š“³öyÓėŹ±¼äxµÄŗÆŹż¹ŲĻµŹ½£¬²¢ÅŠ¶ĻµŚ¼øĢģČÕĻśŹŪ×ÜĮæy×ī“󣬲¢Ēó³ö“ĖŹ±×ī“óÖµ£® 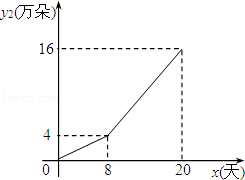
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖaÓėbĀś×ć![]() £¬ŹżÖįÉĻµćA ŗĶµćB Ėł¶ŌÓ¦µÄŹż·Ö±šĪŖaŗĶb£¬µćP ĪŖŹżÖįÉĻŅ»¶Æµć£¬Ęä¶ŌÓ¦µÄŹżĪŖ
£¬ŹżÖįÉĻµćA ŗĶµćB Ėł¶ŌÓ¦µÄŹż·Ö±šĪŖaŗĶb£¬µćP ĪŖŹżÖįÉĻŅ»¶Æµć£¬Ęä¶ŌÓ¦µÄŹżĪŖ![]() £®
£®
£Ø1£©Ēóa,bµÄÖµ£®
£Ø2£©Čōµć P µ½µć A”¢µć B µÄ¾ąĄėĻąµČ£¬ĒóµćP¶ŌÓ¦µÄŹż.
£Ø3£©ĻÖŌŚµć A”¢µć B ·Ö±šŅŌ 2 øöµ„Ī»³¤¶Č/ĆėŗĶ 0.5 øöµ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĶ¬Ź±ĻņÓŅŌĖ¶Æ£¬µć P ŅŌ 3 øöµ„Ī»³¤¶Č/ĆėµÄĖŁ¶ČĶ¬Ź±“ÓŌµćĻņ×óŌĖ¶Æ£®µ±µć A Óėµć B Ö®¼äµÄ¾ąĄėĪŖ2øöµ„Ī»³¤¶ČŹ±£¬Ēóµć P Ėł¶ŌÓ¦µÄŹżŹĒ¶ąÉŁ£æ
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬DEŹĒ¹żµćAµÄÖ±Ļߣ¬BD”ĶDEÓŚD£¬CE”ĶDEÓŚµćE£»
£Ø1£©ČōB”¢CŌŚDEµÄĶ¬²ą£ØČēĶ¼ĖłŹ¾£©ĒŅAD=CE£®ĒóÖ¤£ŗAB”ĶAC£»
£Ø2£©ČōB”¢CŌŚDEµÄĮ½²ą£ØČēĶ¼ĖłŹ¾£©£¬ĘäĖūĢõ¼ž²»±ä£¬ABÓėACČŌ“¹Ö±Āš£æČōŹĒĒėøų³öÖ¤Ć÷£»Čō²»ŹĒ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĒśĻßABŹĒ¶„µćĪŖB£¬ÓėyÖį½»ÓŚµćAµÄÅ×ĪļĻßy=©x2+4x+2µÄŅ»²æ·Ö£¬ĒśĻßBCŹĒĖ«ĒśĻßy= ![]() µÄŅ»²æ·Ö£¬ÓɵćCæŖŹ¼²»¶ĻÖŲø“”°A©B©C”±µÄ¹ż³Ģ£¬ŠĪ³ÉŅ»×é²ØĄĖĻߣ¬µćP£Ø2017£¬m£©ÓėQ£Ø2025£¬n£©¾łŌŚøĆ²ØĄĖĻßÉĻ£¬¹żµćP”¢Q·Ö±š×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖM”¢N£¬Į¬½įPQ£¬ŌņĖıߊĪPMNQµÄĆ껿ĪŖ£Ø £©
µÄŅ»²æ·Ö£¬ÓɵćCæŖŹ¼²»¶ĻÖŲø“”°A©B©C”±µÄ¹ż³Ģ£¬ŠĪ³ÉŅ»×é²ØĄĖĻߣ¬µćP£Ø2017£¬m£©ÓėQ£Ø2025£¬n£©¾łŌŚøĆ²ØĄĖĻßÉĻ£¬¹żµćP”¢Q·Ö±š×÷xÖįµÄ“¹Ļߣ¬“¹×ćĪŖM”¢N£¬Į¬½įPQ£¬ŌņĖıߊĪPMNQµÄĆ껿ĪŖ£Ø £© 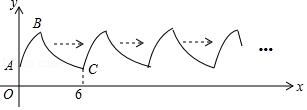
A.72
B.36
C.16
D.9
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬AEŹĒ”ŃOµÄÖ±¾¶£¬µćCŹĒ”ŃOÉĻµÄµć£¬Į¬½įAC²¢ŃÓ³¤ACÖĮµćD£¬Ź¹CD=CA£¬Į¬½įED½»”ŃOÓŚµćB£® 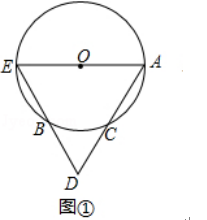
£Ø1£©ĒóÖ¤£ŗµćCŹĒĮÓ»” ![]() µÄÖŠµć£»
µÄÖŠµć£»
£Ø2£©ČēĶ¼¢Ś£¬Į¬½įEC£¬ČōAE=2AC=4£¬ĒóŅõÓ°²æ·ÖµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŌŚÖ±½ĒČż½ĒŠĪABCÖŠ£¬±ßAC³¤4cm£¬±ßBC³¤3cm£¬±ßAB³¤5cm£®
£Ø1£©Čż½ĒŠĪČĘ×űßACŠż×ŖŅ»ÖÜ£¬ĖłµĆ¼øŗĪĢåµÄĢå»żŗĶČĘ×űßBCŠż×ŖŅ»ÖÜĖłµĆ¼øŗĪĢåĢå»żŹĒ·ńŅ»Ńł£æĶعż¼ĘĖćĖµĆ÷£»
£Ø2£©ČōČĘ×űßABŠż×ŖŅ»ÖÜ£¬ĖłµĆµÄ¼øŗĪĢåµÄĢå»żŹĒ¶ąÉŁ£æ

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com