
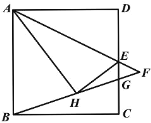
【题目】如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=_______.
【答案】![]()
【解析】
过点H作MN∥AD,交AB于M,交CD于N,通过证明△AMH∽△HNE,可得![]() ,进而得出MH=2EN,HN=
,进而得出MH=2EN,HN=![]() ,可求NE的长,即可求BM,MH,HN的长,由平行线分线段成比例可得HG,GN,EG的长,再次利用平行线分线段成比例可得FG的长.
,可求NE的长,即可求BM,MH,HN的长,由平行线分线段成比例可得HG,GN,EG的长,再次利用平行线分线段成比例可得FG的长.
解:过点H作MN∥AD,交AB于M,交CD于N,
∴∠BAD=∠BMN=90°,∠D=∠MNC=90°,
∴四边形ADNM是矩形,
∴AM=DN,MN=AD=2,
∵将△ADE沿AE折叠至△AHE,
∴AH=AD=2,∠AHE=90°,HE=DE=1,
∴∠AHM+∠EHN=90°,且∠MAH+∠AHM=90°,
∴∠MAH=∠EHN,且∠AMH=∠ENH=90°,
∴△AMH∽△HNE,
∴![]() ,
,
∴![]() ,
,
∴MH=2NE,HN=![]() ,
,
∵MH+HN=MN=2,
∴2NE+![]() =2,
=2,
∴NE=![]() ,
,
∴MH=![]() ,HN=
,HN=![]() ,AM=
,AM=![]() ,
,
∴BM=![]() ,
,
∴BH=![]() ,
,
∵AB∥CD,
∴![]() ,
,
∴NG=![]() ,HG=
,HG=![]() ,
,
∴BG=![]() ,EG=
,EG=![]() ,
,
∵AB∥CD,
∴![]() ,即
,即
∴FG=![]() ,
,
故答案为:![]() .
.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
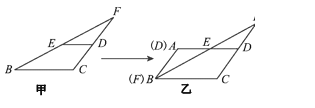
【题目】如图甲,已知ED是△FBC的中位线,沿线段ED将△FED剪下后拼接在图乙中△BEA的位置.
(1)从△FED到△BEA的图形变换,可以认为是(填平移或轴对称或旋转)变换;
(2)试判断图乙中四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是矩形,过点D作DF∥AC交BA的延长线于点F.
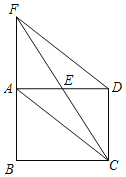
(1)求证:四边形ACDF是平行四边形;
(2)若AB=3,DF=5,求△AEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a<0)经过点A、B.
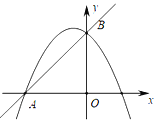
(1)求a、b满足的关系式及c的值.
(2)当x<0时,若y=ax2+bx+c(a<0)的函数值随x的增大而增大,求a的取值范围.
(3)如图,当a=﹣1时,在抛物线上是否存在点P,使△PAB的面积为1?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
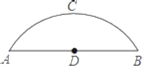
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
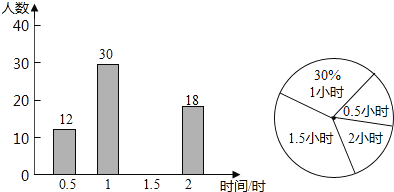
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,四边形
轴的正半轴上,四边形![]() 是平行四边形,
是平行四边形, ![]() ,反比例函数
,反比例函数![]() 在第一象限内的图像经过点
在第一象限内的图像经过点![]() ,与
,与![]() 交于点
交于点![]() ,若点
,若点![]() 为
为![]() 的中点,且
的中点,且![]() 的面积为12,则
的面积为12,则![]() 的值为( )
的值为( )
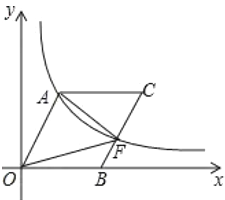
A.16B.24C.36D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市教育局组织部分教师分别到A、B、C、D四个地方进行课程培训,教育局按定额购买了前往四地的车票,如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
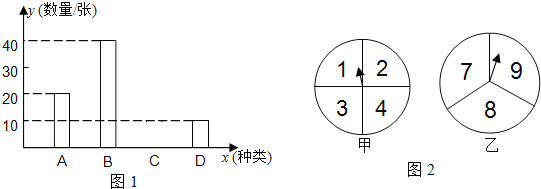
(1)若去A地的车票占全部车票的20%,求去C地的车票数,并补全条形统计图(图1);
(2)请从小到大写出这四类车票数的数字,并直接写出这四个数据的平均数和中位数;
(3)如图2,甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,李老师出去培训,否则张老师出去培训(指针指在线上重转),试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com