
如图,双曲线 (k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为( )
(k≠0)上有一点A,过点A作AB⊥x轴于点B,△AOB的面积为2,则该双曲线的表达式为( )

A.  B.
B.  C.
C.  D.
D. 
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:2018人教版九年级数学下册练习:第二十七章 达标检测卷 题型:单选题
若 ,则
,则 等于( )
等于( )
A. 8 B. 9 C. 10 D. 11
C 【解析】试题解析:设, 则a=2k,b=3k,c=4k, 即, 故选C.查看答案和解析>>
科目:初中数学 来源:浙江杭州建德2016-2017学年七年级上学期期末数学试卷 题型:单选题
已知线段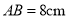 ,在直线
,在直线 上有一点
上有一点 ,且
,且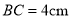 ,点
,点 是线段
是线段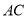 的中点,则线段
的中点,则线段 的长为( ).
的长为( ).
A. 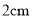 B.
B.  C.
C. 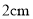 或
或 D.
D.  或
或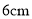
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:填空题
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=6,BC=8.若以点B′,F,C为顶点的三角形与△ABC相似,则BF的长度是______

查看答案和解析>>
科目:初中数学 来源:人教版九年级下册 期中测试卷 题型:单选题
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
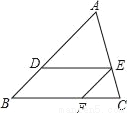
A. 6 B. 8 C. 10 D. 12
C 【解析】∵DE∥BC, ∴∠ADE=∠B,∠AED=∠C, 又∵∠ADE=∠EFC, ∴∠B=∠EFC,△ADE∽△EFC, ∴BD∥EF,, ∴四边形BFED是平行四边形, ∴BD=EF, ∴,解得:DE=10. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:解答题
若代数式(4x2-mx-3y+4)-(8nx2-x+2y-3)的值与字母x的取值无关,求代数式(-m2+2mn-n2)-2(mn-3m2)+3(2n2-mn)的值.
. 【解析】试题分析:已知代数式去括号合并后,根据结果与x的取值无关,求出m与n的值,原式去括号合并后代入数值进行计算即可求出代数式的值. 试题解析:(4x2-mx-3y+4)-(8nx2-x+2y-3) =4x2-mx-3y+4-8nx2+x-2y+3 =(4-8n)x2+(1-m)x-5y+7, ∵上式的值与字母x的取值无关, ∴4-8n=0,1-m=0,即...查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第3章 整式及其加减 单元测试卷 题型:填空题
若-7xm+2y2与-3x3yn是同类项,则m=______,n=______.
1 2 【解析】因为同类项是指所含字母的个数以及相同字母的指数相同,所以m+2=3,n=1, 故答案为:m=1,n=1.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第4章 几何图形初步 单元测试卷 题型:解答题
如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=35°,求∠ACB的度数;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省德州市六校七年级(上)第一次联考数学试卷 题型:单选题
已知:|m﹣2|+(n﹣1)2=0,则方程2m+x=n的解为( )
A. x=﹣4 B. x=﹣3 C. x=﹣2 D. x=﹣1
B 【解析】∵|m﹣2|+(n﹣1)2=0, ∴, ∴, ∴方程可化为: ,解得. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com