练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．只用下列多边形，不能进行平面镶嵌的是（　　）
    A．三角形B．四边形C．正六边形D．正八边形

    分析 几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．360°为正多边形一个内角的整数倍才能单独镶嵌．

    解答 解：A、三角形的内角和为180°，是360°的约数，能镶嵌平面，不符合题意；
    B、四边形的内角和为360°，是360°的约数，能镶嵌平面，不符合题意；
    C、正六边形的一个内角度数为180-360÷6=120°，是360°的约数，能镶嵌平面，不符合题意；
    D、正八边形的一个内角度数为180-360÷8=135°，不是360°的约数，不能镶嵌平面，符合题意．
    故选：D．

    点评 此题考查了平面镶嵌的知识，解题的关键是掌握多边形的一个内角能被360°整除，就能密铺，不能整除，就不能密铺．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．如图，已知⊙O是等腰Rt△ABC的外接圆，点D是$\widehat{AC}$上的一点，BD交AC于点E，若BC=4，AD=$\frac{4}{5}$，则AE的长是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

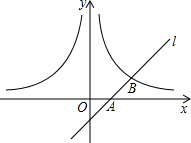    19．如图，直线l经过点A（1，0），且与双曲线y=$\frac{m}{x}$（x＞0）交于点B（2，1），过点P（a，a-1）（a＞1）作x轴的平行线分别交曲线y=$\frac{m}{x}$（x＞0）和y=-$\frac{m}{x}$（x＜0）于M，N两点．
    （1）求m的值及直线l的解析式；
    （2）如果存在点P，使四边形OAMN是平行四边形，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．计算（2$\sqrt{3}$-2$\sqrt{2}$）2=20-8$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．若关于x的一元二次方程（m-2）x2+5x+m2-3m+2=0有一根为0，则m值为（　　）
    A．1B．0C．1或2D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

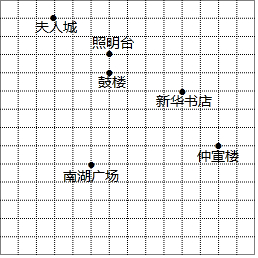    13．周末，小红、小丽、芳芳三位同学相约到仲宣楼游玩，出发前，她们每人带了一张用平面直角坐标系画的示意图，其中新华书店的坐标是（4，-1），南湖广场的坐标是（-1，-5）．
    （1）如图是省略了平面直角坐标系的示意图，请根据上述信息，画出这个平面直角坐标系．
    （2）分别写出夫人城、昭明台、鼓楼、仲宣楼的坐标；
    （3）小红、小丽两个到了鼓楼附近，还没看到芳芳，于是打电话问芳芳的位置，芳芳说她现在的位置坐标是（-2，0），请你在图中用字母A标出芳芳的位置．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如图，点D是△ABC内一点，已知∠ABD=20°，∠BDC=90°，∠ACD=30°，则∠A=40°度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．$\root{3}{-8}$=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某商品现在的售价为每件60元，每星期可卖出100件．市场调查反映：如调整价格，每降价1元，每星期可多卖出20件．已知商品的进价为每件30元，设每件降价x元（x为正整数），每星期的利润为y元．
    （1）求y与x的函数关系式并指出自变量x的取值范围；
    （2）求每星期的利润y的最大值；
    （3）直接写出x在什么范围内时，每星期的利润不低于5000元．

    查看答案和解析>>

    同步练习册答案