练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

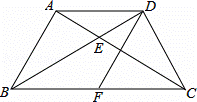
    如图，在四边形ABCD中，AB=AD，AC与BD交于点E，∠ADB=∠ACB．

    （1）求证：=；

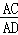    （2）若AB⊥AC，AE：EC=1：2，F是BC中点，求证：四边形ABFD是菱形．


    证明：（1）∵AB=AD，∴∠ADB=∠ABE，又∵∠ADB=∠ACB，∴∠ABE=∠ACB，

    又∵∠BAE=∠CAB，∴△ABE∽△ACB，∴=，又∵AB=AD，∴=；

    （2）设AE=x，∵AE：EC=1：2，∴EC=2x，

    由（1）得：AB2=AE•AC，∴AB=x，又∵BA⊥AC，∴BC=2x，∴∠ACB=30°，

    ∵F是BC中点，∴BF=x，∴BF=AB=AD，

    又∵∠ADB=∠ACB=∠ABD，∴∠ADB=∠CBD=30°，∴AD∥BF，

    ∴四边形ABFD是平行四边形，又∵AD=AB，∴四边形ABFD是菱形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图2，把⊿ABC绕点C按顺时针方向旋转35°，得到⊿A’B’C，A’B’交AC于点D，若∠A’DC=90°，则∠A=

    。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图，在平面直角坐标系xOy中，已知四边形DOBC是矩形，且D（0，4），B（6，0）．若反比例函数y=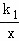（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F．设直线EF的解析式为y=k2x+b．

    （1）求反比例函数和直线EF的解析式；

    （2）求△OEF的面积；

    （3）请结合图象直接写出不等式k2x+b﹣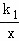＞0的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将两个斜边长相等的三角形纸片如图①放置，其中∠ACB=∠CED=90°，∠A=45°，∠D=30°．把△DCE绕点C顺时针旋转15°得到△D1CE1，如图②，连接D1B，则∠E1D1B的度数为（　　）

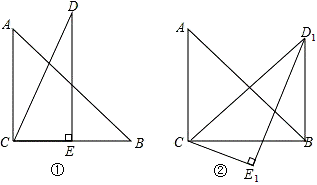
    　  A．10°         B． 20°            C． 7.5°           D． 15°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于D，连接BE．设∠BEC=α，则sinα的值为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     “丝绸之路”经济带首个实体平台——中哈物流合作基地在我市投入使用，其最大装卸能力达410 000标箱，其中“410 000”用科学计数法表示为

    A．0．41×106   B． 4.1×105     C．41×104  D．4.1×104

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个正多边形的一个外角等于30°，则这个正多边形的边数为                 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    的相反数是…………………………………………………………………………（      ）

    A．          B．2           C．           D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，有一矩形纸片ABCD，AB=8，AD=17，将此矩形纸片折叠，使顶点A落在BC边的A′处，折痕所在直线同时经过边AB、AD（包括端点），设BA′=x，则x的取值范围是　　．

     

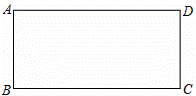
    查看答案和解析>>

    同步练习册答案