
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
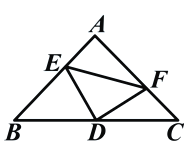
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
【答案】(1)BE=12,CF=5;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)先根据二次根式的非负性求出m=2,再由非负数的性质求出a、b的值,进而得到BE及CF的长;
(2)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到三角形BED与三角形CPD全等,利用全等三角形对应边相等得到BE=CP,再利用SAS得到△EDF和△PDF全等,利用全等三角形对应边相等得到EF=FP,利用等角的余角相等得到∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证;
(3)连接AD,由AB=AC,且D为BC的中点,利用三线合一得到AD垂直于BC,AD为角平分线,再由三角形ABC为等腰直角三角形,得到一对角相等,利用同角的余角相等得到一对角相等,再由AD=CD,利用ASA得到三角形AED与三角形CFD全等,利用全等三角形对应边相等得到AE=CF=5,DE=DF,由AE+EB求出AB的长,即为AC的长,再由AC-CF求出AF的长,在直角三角形AEF中,利用勾股定理求出EF的长,再根据三角形DEF为等腰直角三角形求出DE与DF的长,即可确定出三角形DEF的面积.
试题解析:(1)由题意得![]() ,
,
解得m=2,
则![]() +|b-5|=0,
+|b-5|=0,
所以a-12=0,b-5=0,
a=12,b=5,
即BE=12,CF=5;
(2)延长ED到P,使DP=DE,连接FP,CP,

在△BED和△CPD中,
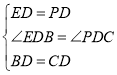 ,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CDP,
在△EDF和△PDF中,
 ,
,
∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴BE2+CF2=EF2;
(3)连接AD,
∵△ABC为等腰直角三角形,D为BC的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∵ED⊥FD,
∴∠EDA+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△AED和△CFD中,
 ,
,
∴△AED≌△CFD(ASA),
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴AB=AE+EB=5+12=17,
∴AF=AC-FC=AB-CF=17-5=12,
在Rt△EAF中,根据勾股定理得:EF=![]() =13,
=13,
设DE=DF=x,
根据勾股定理得:x2+x2=132,
解得:x=![]() ,即DE=DF=
,即DE=DF=![]() ,
,
则S△DEF=![]() DEDF=
DEDF=![]() ×
×![]() ×
×![]() =
=![]() .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
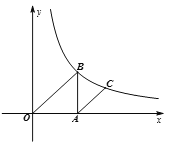
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(a,0)(其中a>0),作AB∥y轴交反比例函数![]() (k>0,x>0)的图象于点B.
(k>0,x>0)的图象于点B.
(1)当△OAB的面积为2时,①求k的值;②若a=2,过A点作AC∥OB交![]() (k>0,x>0)图象于点C,求C的横坐标;
(k>0,x>0)图象于点C,求C的横坐标;
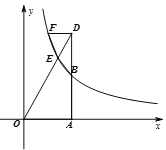
(2)若D为射线AB上一点,连接OD交反比例函数图象于点E,DF∥x轴交反比例函数![]() (k>0,x>0)的图象于点F,连接EF、EB,试猜想:
(k>0,x>0)的图象于点F,连接EF、EB,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
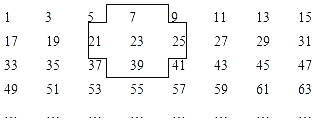
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.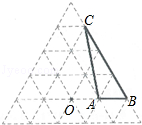
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
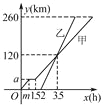
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1…过点A1作y轴的垂线交L2于点A2,过点A2作x轴的垂线交于点A3,过点A3作y轴的垂线交L2于点A4,依次进行下去,则点A2018的坐标为( )
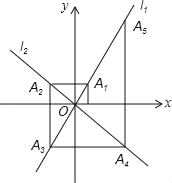
A. (﹣21009,21009) B. (﹣21009,﹣21010)
C. (﹣1009,1009) D. (﹣1009,﹣2018)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com