
 上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE;
上,F是DE上的一点,DF=BE.求证:△ADF≌△ABE; AE.请你说明理由;
AE.请你说明理由; 上.写出线段DE、BE、AE之间的等量关系.(不必证明)
上.写出线段DE、BE、AE之间的等量关系.(不必证明)
 AE,所以只需证明DE-BE=EF即可,由BE=DF不难证明此问题;
AE,所以只需证明DE-BE=EF即可,由BE=DF不难证明此问题;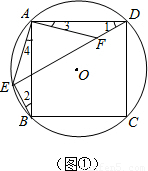 解:(1)在正方形ABCD中,AB=AD(1分)
解:(1)在正方形ABCD中,AB=AD(1分) ,
, ,
, AE.(8分)
AE.(8分) AE.
AE. AE.(9分)
AE.(9分)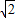 AE.理由如下:(12分)
AE.理由如下:(12分)
 AE.(8分)
AE.(8分)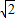 AE.
AE.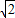 AE.(9分)
AE.(9分)

科目:初中数学 来源: 题型:
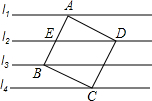 如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于h,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )
如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于h,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )| A、4h2 | ||
| B、5h2 | ||
C、4
| ||
D、5
|
查看答案和解析>>
科目:初中数学 来源: 题型:
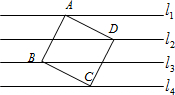 如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )
如图,直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都等于1,若正方形ABCD的四个顶点分别在四条直线上,则它的面积等于( )| A、4 | ||
| B、5 | ||
C、4
| ||
D、5
|
查看答案和解析>>
科目:初中数学 来源: 题型:
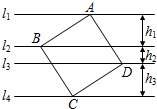 之间的距离依次为h1、h2、h3(h1>0,h2>0,h3>0).
之间的距离依次为h1、h2、h3(h1>0,h2>0,h3>0).| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
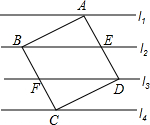 如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,面积是25的正方形ABCD的四个顶点分别在这四条直线上,那么h的值是
如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,面积是25的正方形ABCD的四个顶点分别在这四条直线上,那么h的值是| 5 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com