解:(1)∵二次函数y=mx
2+(m-3)x-3 (m>0)
∴△=(m-3)
2-4(-3)m
=m
2-6m+9+12m
=m
2+6m+9
=(m+3)
2
∵m>0,
∴m+3>3,
∴(m+3)
2>9,
∴(m+3)
2>0,
∴抛物线与x轴有两个不同的交点.
(2)∵y=mx
2+(m-3)x-3=(mx-3)(x+1),
∴x
1=-1,x
2=

,
∴AB=

-(-1)=4,
即m=1;
∴y=x
2-2x-3,
得A(-1,0)、B(3,0)、C(0,-3),
∴∠OBC=45°,∠AMC=90°,
∵AC=

=

,
∵AM=CM,
∴AM=
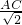
=

,
∴R=

,S=

π.
(3)设PD与BC的交点为E,知道B点、C点的坐标,设直线BC的解析式为y=kx+b

,则有:

,解得:

,
∴直线BC解析式为:y=x-3,
设P(x,x
2-2x-3);当S
△BED:S
△BEP=1:2时,PD=3DE,
得-(x
2-2x-3)=-3(x-3),解得x=2或3,
∴
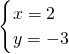
或
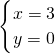
(舍去)
∴P(2,-3);
当S
△PBE:S
△BED=1:2时,同理可得P(

,-

),
故存在P(2,-3)或P(

,-

).
分析:(1)要证明抛物线与x轴有两个不同的交点,只要证明△>就可以了.
(2)根据抛物线的解析式,可表示出A、B的坐标,根据AB=4,可求出m的值,从而确定该抛物线的解析式,即可得到A、B、C的坐标;根据B、C的坐标,可得到∠OBC=45°,根据圆周角定理知∠AMC=90°,即△AMC是等腰直角三角形,AC的长易求得,即可得到半径AM、MC的长,利用扇形的面积公式,即可求得扇形AMC的面积.
(3)设PD与BC的交点为E,此题可分成两种情况考虑:
①当△BPE的面积是△BDE的2倍时,由于△BDE和△BPD同高不等底,那么它们的面积比等于底边的比,即DE=

PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的

,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;
②当△BDE的面积是△BPE的2倍时,方法同①.
点评:此题是二次函数的综合类题目,考查了抛物线的图象与x轴交点坐标的判定、二次函数解析式的确定、圆周角定理的运用、扇形面积的计算方法以及图形面积的求法等知识,综合性强,难度稍大.

 已知二次函数y=mx2+(m-3)x-3 (m>0)
已知二次函数y=mx2+(m-3)x-3 (m>0) ,
, -(-1)=4,
-(-1)=4, =
= ,
,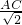 =
= ,
, ,S=
,S= π.
π. ,则有:
,则有: ,解得:
,解得: ,
,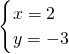 或
或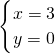 (舍去)
(舍去) ,-
,- ),
), ,-
,- ).
). PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的
PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的 ,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;
,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;

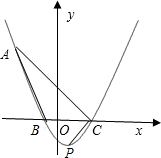 点C,顶点为P.
点C,顶点为P.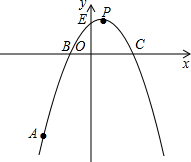 已知二次函数y=-
已知二次函数y=-