
【题目】问题情景:
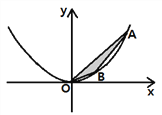
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题:
探究:当a=1时,
mn | m | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
归纳证明:
对任意m、n(m>n>0),猜想S=_________________ (用a,m,n表示),并证明你的猜想.
拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=____ (用a, m,n表示).
【答案】探究:3,15,6,30;归纳证明:猜想:S=![]() amn(m-n);拓展应用:S=
amn(m-n);拓展应用:S=![]() amn(n-m),
amn(n-m),
【解析】试题分析:(1)如图,过点A,B作AD⊥x轴,BC⊥x轴于点D,C,利用![]() ,把所给的值代入求值即可;(2) 猜想:S=
,把所给的值代入求值即可;(2) 猜想:S=![]() amn(m-n),过点A,B作AD⊥x轴,BC⊥x轴于点D、C,表示出A(m,a
amn(m-n),过点A,B作AD⊥x轴,BC⊥x轴于点D、C,表示出A(m,a![]() ),B(n, a
),B(n, a![]() ),利用S=S△AOB=S△AOD-S△OBC-S梯形ABCD,代入证明即可;(3)S=
),利用S=S△AOB=S△AOD-S△OBC-S梯形ABCD,代入证明即可;(3)S=![]() . amn(n-m),类比(2)的方法证明即可.
. amn(n-m),类比(2)的方法证明即可.
试题解析:
探究:3,15,6,30;
归纳证明:
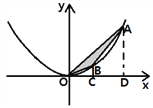
猜想:S=mn(m-n);
证明:过点A,B作Ax轴,BC⊥x轴于点D,C.

∵点A,B的横坐标分别为m,n (m>n>0)
∴A(m,a![]() ),B(n, a
),B(n, a![]() )
)
∴OC=n,BC=a![]() . ,OD=m,AD=a
. ,OD=m,AD=a![]()
∴S=S△AOB=S△AOD-S△OBC-S梯形ABCD
=![]() m×a
m×a![]() -
-![]() n×a
n×a![]() -
-![]() (a
(a![]() +a
+a![]() )(m-n)
)(m-n)
=![]() a
a![]()
![]() n -
n -![]() a
a![]()
![]() m = S=
m = S=![]() amn(m-n),
amn(m-n),
拓展应用:
S=![]() amn(n-m)
amn(n-m)


科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 数据3,4,4,7,3的众数是4
B. 数据0,1,2,5,a的中位数是2
C. 一组数据的众数和中位数不可能相等
D. 数据0,5,-7,-5,7的中位数和平均数都是0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. a不是负数,则a>0 B. b是不大于0的数,则b<0
C. m不小于﹣1,则m>﹣1 D. a,b是负数,则a+ b<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣82+72÷36
(2)2 ![]() ×
× ![]() ÷(﹣9+19)
÷(﹣9+19)
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣36)
)×(﹣36)
(4)1 ![]() ×
× ![]() ﹣(﹣
﹣(﹣ ![]() )×2
)×2 ![]() +(﹣
+(﹣ ![]() )÷1
)÷1 ![]()
(5)﹣13﹣(1﹣0.5)× ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a cm的正方形内,截去两个以正方形的边长a cm为直径的半圆,(结果保留π) 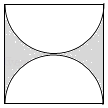
(1)图中阴影部分的周长为cm.
(2)图中阴影部分的面积为cm2 .
(3)当a=4时,求出阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com