
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P�͡�C���������¶��壺�����ڹ���P��ֱ��l����C�����ڵ�P��A��B���㣬��P��A��B�����У�λ���м�ĵ�ǡΪ����������Ϊ�˵���߶ε��е�ʱ����Ƶ�PΪ��C �����ڵ㣬ֱ��lΪ��C���ڵ�P�������ߣ�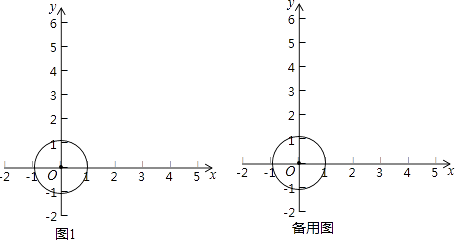
��1������O�İ뾶Ϊ1ʱ��
�ٷֱ��ж��ڵ�D�� ![]() ��
�� ![]() ����E��0����
����E��0���� ![]() ����F��4��0���У��ǡ�O�����ڵ�����
����F��4��0���У��ǡ�O�����ڵ�����
����Ӣ��еĴ��У���ѡһ�����ڵ㣬��ͼ1��������O��������һ�������ߣ���˵�������ͼ���̣�
�۵�P��ֱ��y=��x+3�ϣ�����PΪ��O�����ڵ㣬���P�������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=�� ![]() ��x�ᣬy��ֱ��ڵ�M��N�����߶�MN�ϴ��ڡ�C�����ڵ�P��ֱ��д��Բ��C�ĺ������ȡֵ��Χ��
��x�ᣬy��ֱ��ڵ�M��N�����߶�MN�ϴ��ڡ�C�����ڵ�P��ֱ��д��Բ��C�ĺ������ȡֵ��Χ��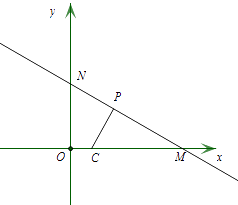
���𰸡�
��1��D��E,�⣺������OD,����D��OD�Ĵ��߽���O��A��B����,��ͼ��ʾ�� 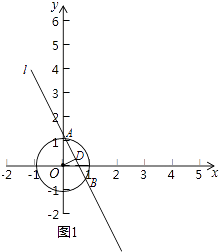 ,����x=0����y=��x+3,��y=3,��y=0����y=��x+3,��x=3,��y=��x+3��������Ľ���Ϊ��0,3���ͣ�3,0�������ڵ�P��ֱ��y=��x+3��,�ҵ�P�ǡ�O�����ڵ�,��0��PO��3,��PO��1�֡ߵ�P�ڡ�O��,��1��PO��3,��p�ĺ����귶ΧΪ��0��x��3��
,����x=0����y=��x+3,��y=3,��y=0����y=��x+3,��x=3,��y=��x+3��������Ľ���Ϊ��0,3���ͣ�3,0�������ڵ�P��ֱ��y=��x+3��,�ҵ�P�ǡ�O�����ڵ�,��0��PO��3,��PO��1�֡ߵ�P�ڡ�O��,��1��PO��3,��p�ĺ����귶ΧΪ��0��x��3��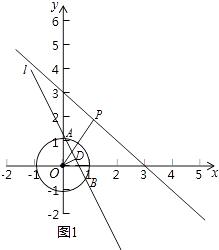
��2���⣺��x=0����y=�� ![]() x+2
x+2 ![]() ��
��
��y=2 ![]() ��
��
��N��0��2 ![]() ����
����
��y=0����y=�� ![]() x+2
x+2 ![]() ��
��
��x=6��
��M��6��0����
�ߵ�P�ǰ뾶Ϊ1�ġ�C�����ڵ㣬
��0��PC��3��PC��1��
���C���Ե�PΪԲ�ģ��뾶Ϊ3��Բ�ڣ��Ҳ������Ե�PΪԲ�ģ��뾶Ϊ1��Բ�ϣ�
�ߵ�C��x���ϣ�
���C�ĺ����귶Χ��ȡֵ��Χ��0��x��9��
���������⣺��1���ɶ����֪��
����P�ڡ�C��ʱ��
�ɴ���������֪����P��Ϊ��C�����ڵ㣬
��ʱ��0��PC��1��
����P�ڡ�C��ʱ��
���A��PB���е㣬
����PC����C�ڵ�M��
�ӳ�PC����C�ڵ�N��
����AM��BN��

�ߡ�AMP+��NMA=180�㣬
��B+��NMA=180�㣬
���AMP=��B��
�ߡ�P=��P��
���AMP�ס�NBP��
�� ![]() =
= ![]() ��
��
��PAPB=PMPN��
�ߵ�A��PB���е㣬
��AB=PA��
�֡ߡ�C�İ뾶Ϊ1��
��2AB2=��PC��CM����PC+CN����
��2AB2=PC2��1��
�֡�AB�ǡ�C���ң�
��AB��2��
��2AB2��8��
��PC2��1��8��
��PC2��9��
��PC��3��
�ߵ�P�ڡ�C�⣬
��PC��1��
��1��PC��3��
����P�ڡ�C��ʱ��
��ʱPC=1�������������⣬
�����������뾶Ϊ1�ġ�C������P��Բ��C�ľ������㣺0��PC��3����PC��1ʱ����PΪ��C�����ڵ㣻
�١�D�� ![]() ��
�� ![]() ����
����
��DO= ![]() =
= ![]() ��
��
��E��0���� ![]() ����
����
��OE= ![]() ��
��
��F��4��0����
��OF=4��
��D��E�ǡ�O�����ڵ㣻


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
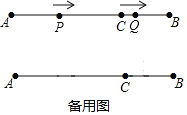
����Ŀ����ͼ��AB=12cm����C���߶�AB�ϣ�AC=3BC������P�ӵ�A��������4cm/s���ٶ������˶��������B֮���������أ���4cm/s���ٶ������˶�������Q�ӵ�C��������1cm/s���ٶ������˶��������B֮���������أ���1cm/s���ٶ������˶���������ͬʱ�������˶�ʱ��Ϊt�룬���ڶ����غ�ʱ��P��Q����ֹͣ�˶���
��1��AC=______cm��BC=______cm��
��2����t=______��ʱ����P���Q��һ���غϣ���t=______��ʱ����P���Q�ڶ����غϣ�
��3����tΪ��ֵʱ��AP=PQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ��� ![]() ��ͼ����
��ͼ���� ![]() .
.
��1����������κ����ĺ�������ʽ��
��2���������߽�x����A,B���㣬��y����C�㣬����ΪD,����A��B��C��DΪ������ı������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
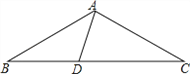
����Ŀ����10�֣���ͼ���ڡ�ABC�У�AB=AC��DΪBC��һ�㣬��B=30��������AD��
��1������BAD=45������֤����ACDΪ���������Σ�
��2������ACDΪֱ�������Σ����BAD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
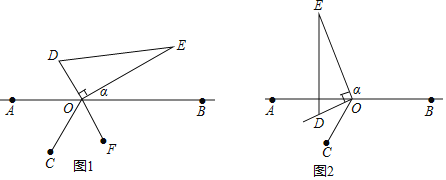
����Ŀ����ͼ1����A��O��B��ͬһֱ���ϣ���AOC=60�㣬��ֱ��AB��һ�ֱ࣬��������DOE��ֱ�Ƕ���O��ʱ����ת����OD��OC�غ�ʱֹͣ�������BOE=����
��1����ͼ1����DO���ӳ���OFƽ�֡�BOC������=______�ȣ�
��2����ͼ2������1����ֱ��������DOE������ʱ����ת����ODλ�ڡ�AOC���ڲ����ҡ�AOD=![]() ��AOC������=__�ȣ�
��AOC������=__�ȣ�
��3��������ֱ��������DOE����ת�����У�����COD+�������Ķ����Ƿ�ı䣿�����ı䣬���������������ı䣬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ٳ�����˵ĸ߶ȣ�С��ͬѧ�뵽������ѧ��ƽ�澵�����ԭ�������ó�����Я���ľ��Ӻ;��ߣ��Ƚ����ӷ��ڽ��µĵ����ϣ�Ȼ����ˣ�ֱ����վֱ���Ӹպ��ܴӾ��������˵Ķ���E����Ǻý�������λ��ΪB����ý�������λ��B����������C�ľ�����50cm����������C������˵ײ�D�ľ���Ϊ4m����ͼ��ʾ����֪С��ͬѧ��������1.54m���۾�λ��A����С��ͷ���ľ�����4cm�������DE�ĸ߶ȵ��ڣ� �� 
A.10m
B.12m
C.12.4m
D.12.32m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У�AB��6��AN��2����BAC��ƽ���߽�BC�ڵ�D��M��AD�ϵĶ��㣬��BM+MN����Сֵ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���⡿
��ͼ�٣���C���߶�AB�ϣ�ͼ�й��������߶�AB��AC��BC����������һ���߶εij���������һ���߶γ��ȵ�2������Ƶ�C���߶�AB�����ɵ���.
�߶ε��е�__________�����߶ε����ɵ���������������������������.
��AB = 12cm����C���߶�AB���ɵ㣬��AC=___________cm��
��������⡿
��3�� ��ͼ�ڣ���֪AB=12cm.����P�ӵ�A��������2cm/s���ٶ���AB���B�����ƶ�����Q�ӵ�B��������1cm/s���ٶ���BA���A�����ƶ�����P��Qͬʱ������������һ�㵽���յ�ʱ���˶�ֹͣ�����ƶ���ʱ��Ϊt��s��.��tΪ��ֵʱ��A��P��Q����������һ��ǡ������������Ϊ�˵���߶ε��ɵ㣿˵������

![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
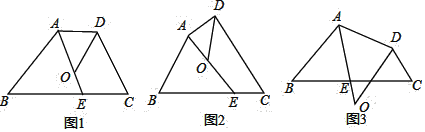
����Ŀ���ı���ABCD�У���BAD�Ľ�ƽ�������BC���ڵ�E����ADC�Ľ�ƽ���߽�ֱ��AE�ڵ�O��
��1������O���ı���ABCD���ڲ���
����ͼ1����AD��BC����B=40�㣬��C=70�㣬���DOE= �㣻
����ͼ2����̽����B����C����DOE֮���������ϵ���������̽������д������
��2����ͼ3������O���ı���ABCD���ⲿ������ֱ��д����B����C����DOE֮���������ϵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com