
分析 (1)两边都除以a2-b2,而a2-b2的值可能为零,由等式的基本性质,等式两边都乘以或除以同一个不为0的整式,等式仍然成立.
(2)根据等式的基本性质和勾股定理,分情况加以讨论
解答 解:(1)上述解题过程从第③步开始出现错误,该步骤的代号为③;
(2)∵a2c2-b2c2=a4-b4,
∴c2(a2-b2)=(a2+b2)(a2-b2),
∴a2-b2=0或c2=a2+b2,
当a2-b2=0时,a=b;
当c2=a2+b2时,∠C=90°,
∴△ABC是等腰三角形或直角三角形.
点评 本题考查了因式分解的应用,勾股定理的逆定理的应用,分类讨论.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.


科目:初中数学 来源: 题型:解答题
 如图,ABCD是等腰梯形,AB∥DC,AD=BC,P是CD上任意一点,过点P作AD、BC的平行线,分别交对角线AC、BD于点E、F,求证:PE+PF=AD.
如图,ABCD是等腰梯形,AB∥DC,AD=BC,P是CD上任意一点,过点P作AD、BC的平行线,分别交对角线AC、BD于点E、F,求证:PE+PF=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
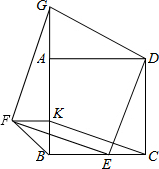 如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.
如图,四边形ABCD是正方形,点E、K分别在DC、AB上,CE=BK,点G在BA的延长线上,DG⊥DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com