
【题目】如图,![]() 是学生小金家附近的一块三角形绿化区的示意图;为增强体质,他每天早晨都沿着绿化区周边小路AB,BC,CA跑步(小路的宽度不计),观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.
是学生小金家附近的一块三角形绿化区的示意图;为增强体质,他每天早晨都沿着绿化区周边小路AB,BC,CA跑步(小路的宽度不计),观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.
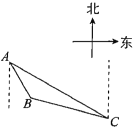
(1)求BC和AB;
(2)小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(结果保留根号)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.

(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
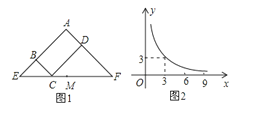
【题目】图(1)所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 满足的反比例函数关系如图(2)所示,等腰直角三角形
满足的反比例函数关系如图(2)所示,等腰直角三角形![]() 的斜边
的斜边![]() 过点
过点![]() ,
,![]() 为
为![]() 的中点,则下列结论正确的是( )
的中点,则下列结论正确的是( )
A. 当![]() 时,
时,![]()
B. 当![]() 时,
时,![]()
C. 当![]() 增大时,
增大时,![]() 的值增大
的值增大
D. 当![]() 增大时,
增大时,![]() 的值不变
的值不变
查看答案和解析>>
科目:初中数学 来源: 题型:
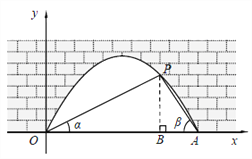
【题目】如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
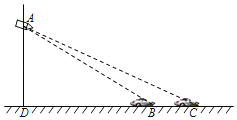
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.
(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数m使关于x的不等式组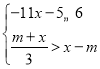 至少有一个非负整数解,且使关于x的分式方程
至少有一个非负整数解,且使关于x的分式方程![]() 有不大于5的整数解,则所有满足条件的m的个数是( )
有不大于5的整数解,则所有满足条件的m的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中秋节”是我国的传统佳节,中秋赏月吃月饼.某蛋糕店销售“杏花楼”和“元祖”两个品牌的月饼,每个“杏花楼”月饼的售价是15元,每个“元祖”月饼的售价是12元.
(1)8月份,两个品牌的月饼一共销售180个,且总销售额不低于2460,则卖出“杏花楼”月饼至少多少个?
(2)9月份,月饼大量上市,受此影响,“杏花楼”月饼的售价降低了a%(a%<30%),销售量在八月份的最低销售量的基础上增加了5a个,“元祖”月饼的售价降低![]() a元,销售量在八份的最高销售量的基础上增加了
a元,销售量在八份的最高销售量的基础上增加了![]() a%,结果9月份的总销售额比8月最低销售额增加了1020元,求a的值.
a%,结果9月份的总销售额比8月最低销售额增加了1020元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:一口袋装有除颜色外均相同的2个红球1个白球和1个篮球,小刚和小明想通过摸球来决定谁去看电影,同学甲设计了如下的方案:第一次随机从口袋中摸出一球(不放回);第二次再任意摸出一球,两人胜负规则如下:摸到“一红一白”,则小刚看电影;摸到“一白一蓝”,则小明看电影.
(1)同学甲的方案公平吗?请用列表或画树状图的方法说明;
(2)你若认为这个方案不公平,那么请你改变一下规则,设计一个公平的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
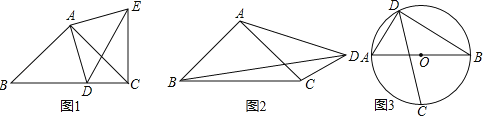
【题目】如图1:在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),试探索AD,BD,CD之间满足的等量关系,并证明你的结论.小明同学的思路是这样的:将线段AD绕点A逆时针旋转90°,得到线段AE,连接EC,DE.继续推理就可以使问题得到解决.
(1)请根据小明的思路,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论;
(2)如图2,在Rt△ABC中,AB=AC,D为△ABC外的一点,且∠ADC=45°,线段AD,BD,CD之间满足的等量关系又是如何的,请证明你的结论;
(3)如图3,已知AB是⊙O的直径,点C,D是⊙O上的点,且∠ADC=45°.
①若AD=6,BD=8,求弦CD的长为 ;
②若AD+BD=14,求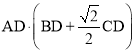 的最大值,并求出此时⊙O的半径.
的最大值,并求出此时⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com