
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
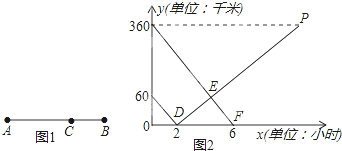
(1)填空:A,B两地相距 千米;货车的速度是 千米/时.
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数表达式;
(3)客、货两车何时相遇?
【答案】(1)A,B两地相距420千米;货车的速度是30千米/时;(2)y2=30x﹣60;(3)客、货两车在出发后![]() 小时相遇.
小时相遇.
【解析】
试题分析:(1)由题意可知:B、C之间的距离为60千米,货车行驶2小时,A、C之间的距离为360千米,所以A,B两地相距360+60=420千米;
(2)根据货车两小时到达C站,求得货车的速度,进一步求得到达A站的时间,进一步设y2与行驶时间x之间的函数关系式可以设x小时到达C站,列出关系式,代入点求得函数解析式即可;
(3)两函数的图象相交,说明两辆车相遇,求得y1的函数解析式,与(2)中的函数解析式联立方程,解决问题.
解:(1)A,B两地相距420千米;货车的速度是30千米/时 …(2分)
(2)设2小时后,货车离C站的路程y2与行驶时间x之间的函数表达式为y2=kx+b,根据题意得
360÷30=12(h),12+2=14(h)
∴点P的坐标为(14,360)…(3分)
将点D(2,0)、点P(14,360)代入y2=kx+b中,![]() …(5分)
…(5分)
解得 k=30,b=﹣60
∴y2=30x﹣60…(6分)
(3)设客车离C站的路程y1与行驶时间x之间的函数表达式为y1=k1x+b1,
根据题意得
![]()
解得k1=﹣60,b1=360
y1=﹣60x+360
由y1=y2得
30x﹣60=﹣60x+360
解得x=![]()
答:客、货两车在出发后![]() 小时相遇.
小时相遇.


科目:初中数学 来源: 题型:
【题目】已知,如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s,点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ,若设运动的时间为t(s)(0<t<2),解答下列问题:
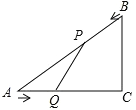
(1)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(2)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州休博会期间,嘉年华游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收33万元.而该游乐设施开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx;若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数;
(1)若维修保养费用第1个月为2万元,第2个月为4万元.求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大;几个月后,能收回投资?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com