
����Ŀ��ƽ��ֱ������ϵ�У���A��B��C���㣬����AΪԭ�㣬��B�͵�C������ֱ�Ϊ��5,0���ͣ�1,2��.
��1��֤������ABCΪRT����
��2��������ֱ������ϵ����һ��D��ʹ����ABC����ABD���ƣ�д���������������ĵ�D�����꣬����ͬһ����ϵ�л������з���Ҫ��������Σ�
��3���ڵڣ�2����������ͼ�У�������������ֱ�������Σ�������ABC����ֱ�Ƕ�����ɵõ�һ���߶Σ��������������õ������߶�����ȡһ���߶Σ���ȡ������Ϊ���������߶εĸ���.
���𰸡���1��֤������������2��D1��1��-2����D2��4��-1����D3��4��1����D4��5��-10����D5��5��10����D6��5��-2.5����D7��5��2.5����D8��0��-10����D9��0��10����D10��0��-2.5����D11��0��2.5������ͼ����������3��p=![]() .
.
��������
���������������Ҫ�����˹��ɶ��������涨�������������ε����ʡ����ʹ�ʽ��֪ʶ�����÷������۵�˼���ǽ���ڣ�2��С��Ĺؼ���
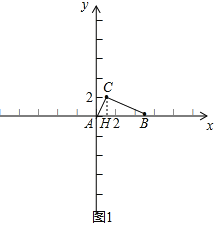
��1������C��CH��x����H����ͼ1��ֻ�����ù��ɶ������AB2��AC2��BC2��Ȼ�����ù��ɶ������涨���Ϳɽ�����⣻
��2����ABC���ABD���ƣ���Ӧ��ϵ��ȷ������������������������ABC�ס�ABD��������ABC�ס�BAD��������ABC�ס�ADB��������ABC�ס�DAB��������ABC�ס�BDA��������ABC�ס�DBA�����ۣ�Ȼ���������������ε����ʾͿɽ�����⣻
��3��ͼ�е�ֱ�������ε�ֱ�Ƕ�����A��B��C��D1��D2��D3��ֻ�����������ֱ�Ƕ�������߶ε������ͳ���Ϊ���������߶ε��������Ϳɽ�����⣮
�����������1������C��CH��x����H����ͼ1��
��A��0��0����B��5��0����C��1��2����
��AC=![]() ��BC=2
��BC=2![]() ��AB=5��
��AB=5��
��AB2=AC2+BC2��
���ABCΪRT����
 ��
��
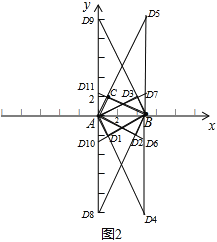
��2��������ABC�ס�ABD������D1��1��-2����
������ABC�ס�BAD������D2��4��-1����D3��4��1����
������ABC�ס�ADB������D4��5��-10����D5��5��10����
������ABC�ס�DAB������D6��5��-2.5����D7��5��2.5����
������ABC�ס�BDA������D8��0��-10����D9��0��10����
������ABC�ס�DBA������D10��0��-2.5����D11��0��2.5����
���з���Ҫ�����������ͼ2��ʾ��
 ��
��
��3��ͼ�е�ֱ�������ε�ֱ�Ƕ�����A��B��C��D1��D2��D3��
������ֱ�Ƕ�������߶ι���6��52=15����
����AB=5��CD1=D2D3=4��CD2=D1D3=5��CD3=D1D2=3��
�ʳ���Ϊ���������߶ι�7��������Ϊ���������߶ι�8����
��ȡ������Ϊ���������߶εĸ���Ϊp=![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��Ϊ���˽�������С����Լ��3000�ˣ�������˶������������Ӧ���õ��ռ����ݵķ�ʽ�ǣ�������
A. ��С�����г����˷��ʾ�����
B. ��С����������Сѧ�����ʾ�����
C. ��С���������������ʾ����е���
D. ���Ұ������ʾ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ������b��cΪ������c��0���Ķ���ǡΪ����
������b��cΪ������c��0���Ķ���ǡΪ����![]() ��
��![]() ������һ������.��
������һ������.��![]() ��
��![]() ��
��![]() ʱ��a��ȡֵ��Χ�� .
ʱ��a��ȡֵ��Χ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ǻ�����2016��2�·ݵĿ�������ָ����AQI����ͳ��ͼ����������ָ��AQI��ֵ�ڲ�ͬ�����䣬�ʹ����˲�ͬ�Ŀ�������ˮƽ������0�C50֮�䣬������������51�C100֮�䣬������������101�C150֮�䣬�����������Ⱦ���ȡ��������ǹ��ں�����2016��2�·ݿ��������������ͳ��ͼ.
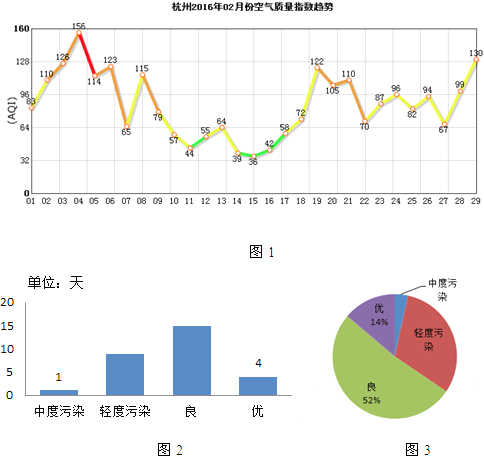
��1����������ͼ���е���Ϣ���벹ȫ����ͳ��ͼ������ͳ��ͼ��ȱʧ�����ݣ�������ͳ��ͼ�е����ݾ�ȷ��1%��
��2�����ͼ3�б�ʾ�����Ⱦ������Բ�ĽǵĶ�����(�����ȷ����)
��3���ں��ݣ���һ�������������������������ڵ�һ���У����������г���һ�����ϵ�ʱ���ܿ�������������.�����2016��һ�꺼�ݵĿ�������Ϊ����������.��һ�갴365�ƣ���ȷ���죩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧ������Ϊ�˽ⱾУѧ��ϲ�������˶�������������ȡ��������ѧ�������ʾ����飬Ҫ��ÿλѧ��ֻ����дһ���Լ�ϲ���������˶�����������Ľ�����Ƴ����µ�������������ͳ��ͼ��
�����ͳ��ͼ���ṩ����Ϣ������������⣺

��1���μӵ������������ �ˣ�������ͼ�У�m= ��������ͼ����������
��2�������У��3500��ѧ���������ϲ��������ѧ�����ж����ˣ�
��3�������żƻ������������ƹ�����У������ȡ����������֯������������״ͼ���б��������ȡ������������ǡ���ǡ����͡����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=-2��x-3��2-1�Ķ��������ǣ�������
A. ��3��1�� B. ��3����1�� C. ����3��1�� D. ����3����1��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com