
如图,已知△BEC 是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC、BD的交点为O。
(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2cm ,求图中阴影部分的面积。
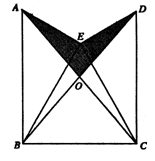
解:(1)∵∠AEB=∠DEC=90°,
∴∠AEB+ ∠BEC=∠DEC+∠BEC,
即∠AEC=∠DEB,
∵△BEC是等边三角形,
∴CE=BE,
又AE=DE,
∴△AEC≌△DEB;
(2)连结EO并延长EO交BC于点F,连结AD,
由(1),知AC=BD,
∵∠ABC=∠DCB=90°,
∴∠ABC+∠DCB=180°,AB∥DC,
AB=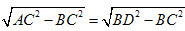 =CD,
=CD,
∴四边形ABCD为平行四边形且矩形,
∴OA=OB=OC=OD,
又∵BE=CE,
∴OE所在直线垂直平分线段BC,
∴BF=FC,∠EFB=90°,
∴OF= AB=
AB=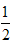 ×2=1,
×2=1,
∵△BEC是等边三角形,
∴∠EBC=60°,
在Rt△AEB中,
∠AEB=90°,∠ABE=∠ABC-∠EBC=90°-60°=30°,
∴BE=AB·cos30°=2× ,
,
在Rt△BFE中,∠BFE=90°,∠EBF=60°,
∴BF=BE·cos60°= ,
,
EF=BE·sin60°= ,
,
∴OE=EF-OF= ,
,
∵AE=ED,OE=OE,AO=DO,
∴△AOE≌△DOE,
∴S △AOE=S△DOE,
∴S=2S△AOE =2×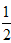 ·EO·BF=2×
·EO·BF=2×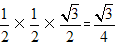 (cm2)。
(cm2)。


科目:初中数学 来源: 题型:
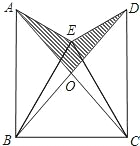 如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
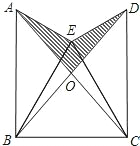 如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.查看答案和解析>>
科目:初中数学 来源:第21章《解直角三角形》中考题集(22):21.4 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第4章《锐角三角形》中考题集(26):4.3 解直角三角形及其应用(解析版) 题型:解答题
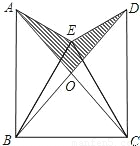
查看答案和解析>>
科目:初中数学 来源:2006年江苏省南通市中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com