

| A. | 9,10 | B. | 9,91 | C. | 10,91 | D. | 10,110 |
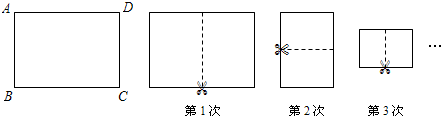
分析 分析前三个正方形,发现“右上的数=左上的数+3,左下的数=左上的数+4,右下的数=右上的数×右下的数+1”,依此即可得出a、b、c的值.
解答 解:分析正方形中的四个数:
∵第一个正方形中0+3=3,0+4=4,3×4+1=13;第二个正方形中2+3=5,2+4=6,5×6+1=31;第三个正方形中4+3=7,4+4=8,7×8+1=57.
∴c=6+3=9,a=6+4=10,c=9×10+1=91.
故选C.
点评 本题考查了规律型中的数字的变换类,解题的关键是分析正方形中四个数找出它们之间的关系“右上的数=左上的数+3,左下的数=左上的数+4,右下的数=右上的数×右下的数+1”.本题属于基础题,难度不大,解决该题型题目时,根据给定的正方形中的4个数,找出它们之间的关系是关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
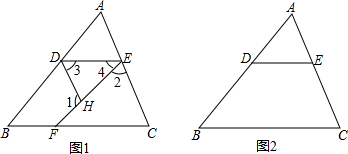 如图1,△ABC中,D,E,F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C.
如图1,△ABC中,D,E,F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com