
【题目】计算
(1)![]() ;
;
(2)![]()
;
(3)![]()
(4)![]()
(5)![]()
(6)![]()
(7)![]() .
.![]()
【答案】
(1)
解:原式=4-1+9=12.
(2)
解:原式=(100+1)(100-1)=1002-1=9999.
(3)
解:原式=[-2×(-1)×![]() ]x5y6=
]x5y6=![]() x5y6
x5y6
(4)
解:原式=5x3-10x2-5x.
(5)
解:原式=10x-2x3+15-3x2=-2x3-3x2+10x+15.
(6)
解:原式=b2-4a2-(a2-6ab+9b2)=b2-4a2-a2+6ab-9b2=-8b2+6ab-5a2
(7)
解:原式=(a-3b)2-c2=a2-6ab+9b2-c2
【解析】(1)负整数指数幂,零指数幂;
(2)运用平方差公式简便运算;
(3)~(7)是整式的乘法,可运用平方差和完全平方公式进行简便运算.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对整数指数幂的运算性质的理解,了解aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点,则: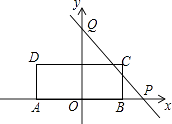
(1)a的取值范围是;
(2)若设直线PQ为:y=kx+2(k≠0),则此时k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点的位置如图所示,将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
利用网格点画图: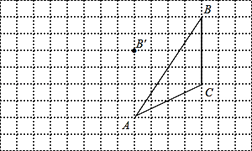
(1)画出△A′B′C′;
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD中∠BAD=α,∠BCD=β, BE、DF分别平分四边形的外角∠MBC和∠NDC
(1)如图1,若α+β= ![]() ,则∠MBC+∠NDC=度;
,则∠MBC+∠NDC=度;
(2)如图1,若BE与DF相交于点G,∠BGD=45°,请求出α、β所满足的等量关系式;
(3)如图2,若α=β,判断BE、DF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com