
【题目】下列变量之间关系中,一个变量是另一个变量的正比例函数的是( )
A.正方形的面积S随着边长x的变化而变化
B.正方形的周长C随着边长x的变化而变化
C.水箱有水10升,以0.5升/分的流量往外放水,剩水量(升)随着放水时问t(分)的变化而变化
D.面积为20的三角形的一边a随着这边上的高h的变化而变化
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
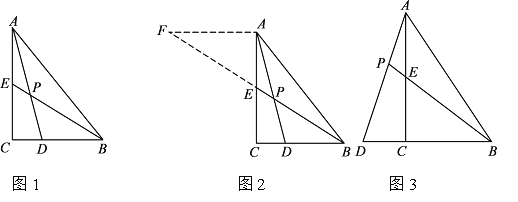
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求![]() 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答:![]() 的值为 .
的值为 .
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求![]() 的值;
的值;
(2)若CD=2,则BP=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个问题解决往往经历发现猜想——探索归纳——问题解决的过程,下面结合一道几何题来体验一下.
(发现猜想)(1)如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;.


(探索归纳)(2)如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线. 猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
(问题解决)(3)如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动. 运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学图书馆上周借书记录如下(以100册为标准,超过的册数记为正,不足的册数记为负):

(1)上星期五借出多少册?
(2)上星期四比上星期三多借出多少册?
(3)上周平均每天借出多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)计算:6÷(-![]() +
+![]() ).
).

方方同学的计算过程如下:原式=6÷(-![]() )+6÷
)+6÷![]() =-12+18=6.
=-12+18=6.
请你判断方方同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考黑板中老师的讲解,用运算律简便计算(请写出具体的解题过程):
①999×(-15);②999×![]() +333×(-
+333×(-![]() )-999×
)-999×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )

A. 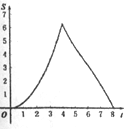 B.
B. 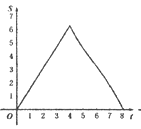
C. 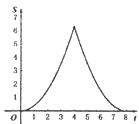 D.
D. 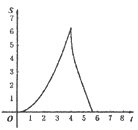
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在网上销售苹果,原计划每天卖100斤,但实际每天的销量与计划销量相比有出入,如表是某周7天的销售情况(超额记为正,不足记为负.单位:斤):

(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 斤;
(2)本周实际销售总量达到了计划销量没有?
(3)若每斤按5元出售,每斤苹果的运费为1元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蛋糕店为了吸引顾客,在A、B两种蛋糕中,轮流降低其中一种蛋糕价格,这样形成两种盈利模式,模式一:A种蛋糕利润每盒8元,B种蛋糕利润每盒15元;模式二:A种蛋糕利润每盒14元,B种蛋糕利润每盒11元每天限定销售A、B两种蛋糕共40盒,且都能售完,设每天销售A种蛋糕x盒
(1)设按模式一销售A、B两种蛋糕所获利润为y1元,按模式二销售A、B两种蛋糕所获利润为y2元,分别求出y1、y2关于x的函数解析式;
(2)在同一个坐标系内分别画出(1)题中的两个函数的图象;

(3)若y始终表示y1、y2中较大的值,请问y是否为x的函数,并说说你的理由,并直接写出y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com