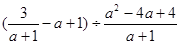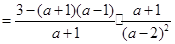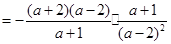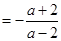试题分析:(1)观察可得最简公分母是x(x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(2)首先把方程移项变形为x2+4x=1的形式,然后在方程的左右两边同时加上一次项系数一半的平方,左边就是完全平方式,右边就是常数,然后直接开平方即可求解.
(3)这是个分式除法与减法混合运算题,运算顺序是先做括号内的加法,此时要先确定最简公分母进行通分;做除法时要注意先把除法运算转化为乘法运算,而做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分.化简后选一个适当的数代入求值即可.
试题解析:(1)原方程两边同乘x(x-1),
得x
2+x-1=x(x-1),
展开、整理得2x=1,
解得x=
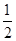
.
将x=
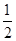
代入x(x-1)=
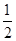
×(
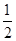
-1)=-
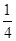
≠0.
∴原方程的解为x=
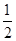
.
(2)x
2+4x-1=0,
移项得,x
2+4x=1,
配方得,x
2+4x+4=1+4,
(x+2)
2=5,
开方得,x+2=±
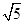
,
解得,x
1=-2+
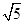
,x
2=-2-
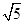
.
(3)
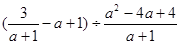
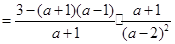
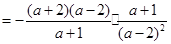
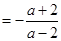
当a=0时,原式=1.
考点:1.解分式方程;2.解一元二次方程---配方法; 3.分式的混合运算.

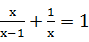 ②
②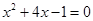
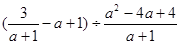 ,并从0,
,并从0,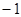 ,2中选一个合适的数作为
,2中选一个合适的数作为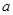 的值代入求值.
的值代入求值.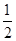 ;(2)x1=-2+
;(2)x1=-2+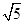 ,x2=-2-
,x2=-2-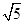 ;(3)当a=0时,原式=1.
;(3)当a=0时,原式=1.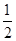 .
.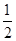 代入x(x-1)=
代入x(x-1)=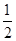 ×(
×(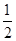 -1)=-
-1)=-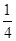 ≠0.
≠0.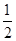 .
.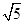 ,
,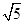 ,x2=-2-
,x2=-2-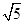 .
.