
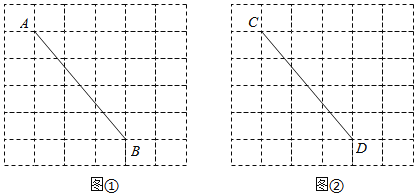
【题目】图①、图②均是6×6的正方形网格,每个小正方形的边长为1,小正方形的顶点称为格点,点A、B、C、D均在格点上.用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写画法.
(1)在图①中以线段AB为腰画一个等腰三角形ABM,画出的△ABM的面积是 .
(2)在图②中以线段CD为边画一个四边形CDEF,使∠FCD+∠EDC=90°.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D是边BC上一动点(不与B、C重合),
,点D是边BC上一动点(不与B、C重合),![]() ,DE交AC于点E,且
,DE交AC于点E,且![]() .下列结论:①
.下列结论:①![]() ∽
∽![]() ;②当
;②当![]() 时,
时,![]() 与
与![]() 全等;③
全等;③![]() 为直角三角形时,BD等于8或
为直角三角形时,BD等于8或![]() .其中正确的有__________.(选填序号)
.其中正确的有__________.(选填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
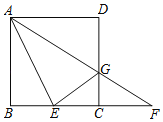
【题目】如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设![]() =λ(λ>0).
=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
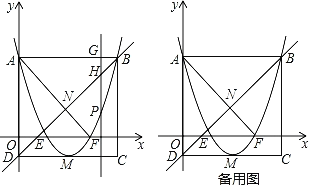
【题目】如图,抛物线y=x2+bx+c经过A (0,3),B (4,3)两点,与x轴交于点E,F,以AB为边作矩形ABCD,其中CD边经过抛物线的项点M,点P是抛物线上一动点(点P不与点A,B重合),过点P作y轴的平行线1与直线AB交于点G,与直线BD交于点H,连接AF交直线BD于点N.
(1)求该抛物线的解析式以及顶点M的坐标;
(2)当线段PH=2GH时,求点P的坐标;
(3)在抛物线上是否存在点P,使得以点P,E,N,F为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.

(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.动点P从点A出发,沿AB以每秒5个单位长度的速度向终点B运动.当点P不与点A重合时,过点P作PD⊥AC于点D、PE∥AC,过点D作DE∥AB,DE与PE交于点E.设点P的运动时间为t秒.
(1)线段AD的长为 .(用含t的代数式表示).
(2)当点E落在BC边上时,求t的值.
(3)设△DPE与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式.
(4)若线段PE的中点为Q,当点Q落在△ABC一边垂直平分线上时,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对九年一班50名学生进行长跑项目的测试,根据测试成绩制作了两个统计图.

请根据相关信息,解答下列问题:
(1)本次测试的学生中,得3分的学生有________人,得4分的学生有________人;
(2)求这50个数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2022年北京冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作,北京冬残奥会吉祥物“雪容融”则以中国标志性符号的灯笼为创意进行设计创作“冰墩墩”和“雪容融”是一个非常完美的搭:配和组合,是中国文化和奥林匹克精神又一次完美的结合莉莉有“冰墩墩”和“雪容融”的纪念邮票各2张(如图),这4张邮票背面完全相同,莉莉想给好友小婷和小华各送一张纪念邮票,她先让小婷从这4张邮票中随机抽取一张,然后,再让小华从剩下的3张中随机抽取一张.

(1)小婷抽到“冰墩墩”的纪念邮票的概率是__________.
(2)利用树状图或列表法求小婷和小华均抽到“雪容融”的纪念邮票的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
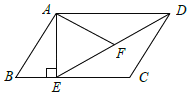
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com