
【题目】生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二,产生新的微生物(依次被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么标号为1000的微生物会出现在( )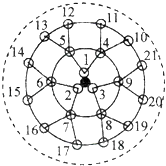
A.第7天
B.第8天
C.第9天
D.第10天
【答案】B
【解析】解:第一天产生新的微生物有6个标号,
第二天产生新的微生物有12个标号,
以此类推,第三天、第四天、第五天…产生新的微生物分别有24个,48个,96个,192个,384个,768个,…
前八天所有微生物的标号共有3+6+12+24+48+96+192+384=762个,
所以标号为1000的微生物会出现在第8天.
故选:B.
由图和题意可知,第一天产生新的微生物有6个标号,第二天产生新的微生物有12个标号,以此类推,第三天、第四天、第五天产生新的微生物分别有24个,48个,96个,192,384,768,…而前八天所有微生物的标号共有3+6+12+24+48+96+192+384=762个,由此推出标号为1000的微生物会出现在第8天.


科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 A=3x3+2x2﹣5x+7m+2,B=2x2+mx﹣3,若多项式 A+B 不含一次项,则多项式 A+B 的常数项是( )
A. 16 B. 24 C. 34 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
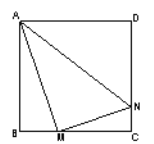 (3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com