

分析 (1)如图1中,作DH⊥AB于H.在Rt△ADH中,由∠AHD=90°,AD=5,cos∠DAH=$\frac{3}{5}$,推出AH=3,DH=$\sqrt{{5}^{2}-{3}^{2}}$=4,即可解决问题;
(2)如图1中,BD与AC交于点G.在Rt△DHB中,可得BD=$\sqrt{D{H}^{2}+B{H}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,由四边形ABCD是菱形,推出AC⊥BD,BG=DG=$\sqrt{5}$,AG=$\sqrt{A{B}^{2}-B{G}^{2}}$=$\sqrt{{5}^{2}-(\sqrt{5})^{2}}$=2$\sqrt{5}$,由△AEF∽△AGB,推出$\frac{AE}{AF}$=$\frac{AG}{BG}$=$\frac{2\sqrt{5}}{\sqrt{5}}$=2,即可解决问题;
(3)分三种情形分别求解:①如图2中,当⊙O与直线DF相切时.②如图3中,当⊙O与AC相切时.③如图4中,当⊙O与CD相切于点M.分别求解即可;
解答 (1)解:如图1中,作DH⊥AB于H.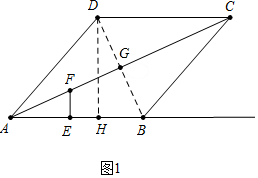
在Rt△ADH中,∵∠AHD=90°,AD=5,cos∠DAH=$\frac{3}{5}$,
∴AH=3,DH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴S菱形ABCD=AB•DH=5×4=20.
(2)证明:如图1中,BD与AC交于点G.
在Rt△DHB中,∵DH=4,BH=2,
∴BD=$\sqrt{D{H}^{2}+B{H}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵四边形ABCD是菱形,
∴AC⊥BD,BG=DG=$\sqrt{5}$,AG=$\sqrt{A{B}^{2}-B{G}^{2}}$=$\sqrt{{5}^{2}-(\sqrt{5})^{2}}$=2$\sqrt{5}$,
∵∠EAF=∠BAG,∠AEF=∠AGB=90°,
∴△AEF∽△AGB,
∴$\frac{AE}{AF}$=$\frac{AG}{BG}$=$\frac{2\sqrt{5}}{\sqrt{5}}$=2,
∴AE=2EF.
(3)解:①如图2中,当⊙O与直线DF相切时,易知,∠BFD=90°,DF=BF.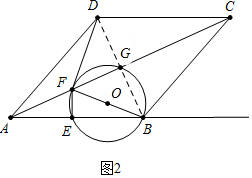
∵BD=2$\sqrt{5}$,
∴BF=$\sqrt{10}$,设EF=x,则AE=2EF=2x,
在Rt△BEF中,∵BF2=EF2+BE2,
∴10=x2+(5-2x)2,
解得x=1或3,
∴AE=2或6时,⊙O与直线DF相切.
②如图3中,当⊙O与AC相切时,易知点F与G重合,设EF=x,AE=2x,
在Rt△AFE中,∵AG2=AE2+GE2,
∴20=4x2+x2,
∴x2=4,
∴x=2,
∴AE=4时,⊙O与直线CF相切.
③如图4中,当⊙O与CD相切于点M,延长MO交AE与H,设EF=x,则AE=2x,则OH=$\frac{1}{2}$EF=$\frac{1}{2}$x,BF=$\sqrt{{x}^{2}+(2x-5)^{2}}$,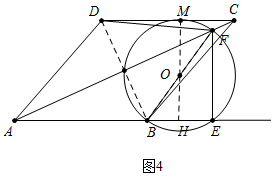
∵HM=4,
∴OM+OH=4,
∴$\frac{1}{2}$$\sqrt{{x}^{2}+(2x-5)^{2}}$+$\frac{1}{2}$x=4,
整理得,4x2-4x-39=0,
解得x=$\frac{1+2\sqrt{10}}{2}$或$\frac{1-2\sqrt{10}}{2}$(舍弃),
∴AE=1+2$\sqrt{10}$,
综上所述,满足条件的AE的值为2或4或6或1+2$\sqrt{10}$.
点评 本题考查圆综合题、菱形的性质、直线与圆的位置关系、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:解答题
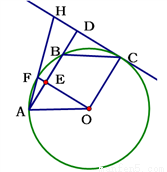
如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D, 延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)求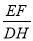 的比值;若DH=6,求EF和半径OA的长.
的比值;若DH=6,求EF和半径OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:解答题
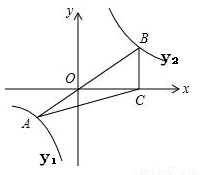
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数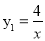 (x<0)图象上一点,AO的延长线交函数
(x<0)图象上一点,AO的延长线交函数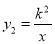 (x>0,k<0)的
(x>0,k<0)的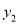 图象于点B,BC⊥x轴,若S△ABC=
图象于点B,BC⊥x轴,若S△ABC=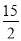 ,求函数y2的解析式.
,求函数y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com