
分析 根据题意,通过列表分析可得两个骰子的点数情况,投掷两个均匀的骰子,所有可能出现的结果共有36种,
若m、n为奇数,m为奇数有3种情况,n为奇数有3种情况,所以两枚骰子朝上的点数都是奇数有3×3=9种情况;
求两枚骰子朝上的点数都是奇数的可能性,根据可能性的求法:即求一个数是另一个数的几分之几用除法解答即可.
解答 解:列表如下:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
点评 此题考查可能性问题,解答此题应根据可能性的求法:即求一个数是另一个数的几分之几用除法解答,进而得出结论.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
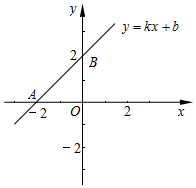 如图是一次函数y=kx+b的图象.
如图是一次函数y=kx+b的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥CD,BC=CD=10,sin∠BDC=$\frac{4}{5}$,∠ADB=90°,点E为边AB的中点,点F为线段CD上的一动点(点F不与C、D重合),联结FE,与BD相交于点G,点P为边AD上一点,且PE⊥EF.设BG=x,AP=y.
如图,在梯形ABCD中,AB∥CD,BC=CD=10,sin∠BDC=$\frac{4}{5}$,∠ADB=90°,点E为边AB的中点,点F为线段CD上的一动点(点F不与C、D重合),联结FE,与BD相交于点G,点P为边AD上一点,且PE⊥EF.设BG=x,AP=y.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
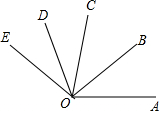 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=38°,∠COE=62°,则∠BOD的度数为( )| A. | 50° | B. | 62° | C. | 69° | D. | 76° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com