
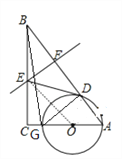
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点O在AC上,OA=2,以OA为半径的⊙O交AB于点D,AC于G,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)求证:直线DE是⊙O的切线;
(2)求线段DE的长;
(3)求线段AD的长.
【答案】(1)证明见解析(2)DE=4.75(3)2.4
【解析】试题分析:(1)连接OD,欲证DE是切线,只要证明OD⊥DE即可;
(2)连接OE,设DE=BE=x,CE=8﹣x,利用勾股定理求解即可;
(3)连结BG,DG,根据三角形的面积的不同求法,然后根据勾股定理求解.
试题解析:(1)连接OD,
∵EF垂直平分BD,∴EB=ED,
∴∠B=∠EDB,
∵OA=OD,∴∠ODA=∠A,
∵∠C=90°,∴∠A+∠B=90°,
∴∠EDB+∠ODA=90°,∴∠ODE=90°,
∴OD⊥DE于D,∴DE是⊙O的切线.
(2)连接OE,
设DE=BE=x,CE=8﹣x,
∵OE2=DE2+OD2=EC2+OC2,
∴42+(8﹣x)2=22+x2,
解得x=4.75,
 ∴DE=4.75.
∴DE=4.75.
(3)连结BG,DG.
∵AG是直径,∴GD⊥AB
由S△ABG=![]() AG·BC=
AG·BC=![]() AB·GD可得:4×8=10×GD,
AB·GD可得:4×8=10×GD,
∴GD=3.2
∴AD=![]() =2.4
=2.4


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
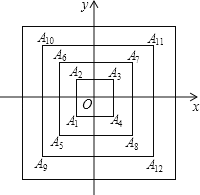
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小亮上山游玩,小颗乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颗在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米。图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:cm)的最大值为175,最小值为155.若取组距为3,则可以分成____组.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个命题:
①、同位角相等;②、如果两个角的和是 180 度,那么这两个角是邻补角;
③、在同一平面内,平行于同一条直线的两条直线互相平行;
④、在同一平面内,垂直于同一条直线的两条直线互相垂直. 其中是真命题的个数有( )个
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P(﹣1,2)是由点Q(0,﹣1)经过( )而得到的.
A.先向右平移1个长度,再向下平移3个单位长度
B.先向左平移1个长度,再向下平移3个单位长度
C.先向上平移3个长度,再向左平移1个单位长度
D.先向下平移1个长度,再向右平移3个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的面积是60,请完成下列问题:
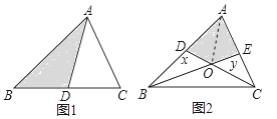
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积________△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO , 同理:S△CEO=S△AEO , 设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程组为:
S△ABC=30,可列方程组为: ![]() , 解得
, 解得![]() ,通过解这个方程组可得四边形ADOE的面积为________ .
,通过解这个方程组可得四边形ADOE的面积为________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2.其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2.其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com